Question

از نقطه تلاقی اقطار ذوزنقه ABCD خطی موازی قاعده ها ( به طول a و b) رسم می کنیم تا ساقها را در K و L قطع کند طول KL بر حسب a و b بیابید

Answer 1

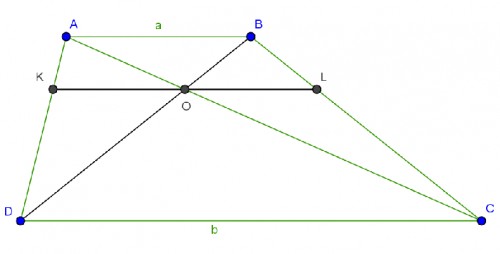
باتوجه به تعمیم تالس : $ \frac{KO}{a}=\frac{KD}{AD} \Rightarrow \color{green}{\frac{a-KO}{a}}=\color{blue}{\frac{AK}{AD}} و \color{green}{\frac{KO}{b}}=\color{blue}{\frac{AK}{AD}} $

بامساوی قراردادن دو طرف تساوی های بالا $$ab=KO(a+b) \Rightarrow \color{RED}{KO= \frac{ab}{a+b}} $$

به طریقه مشابه $$ab=OL(a+b) \Rightarrow \color{RED}{OL= \frac{ab}{a+b}} $$

با نتایج بالا نقطه $O$ وسط $KL$ است وبا جمع طرفین آنها باهم:

$$\color{RED}{KL=\frac{2ab}{a+b}}$$