Question

دو پاره خط EF و GH با قاعده ذوزنقه ABCD موازی می باشند بطوریکه EF ذوزنقه به دو قسمت همساحت و GH ذوزنقه را به دو شکل متشابه تقسیم می کند رابطه بین EF و GH رابیابید

Answer 1

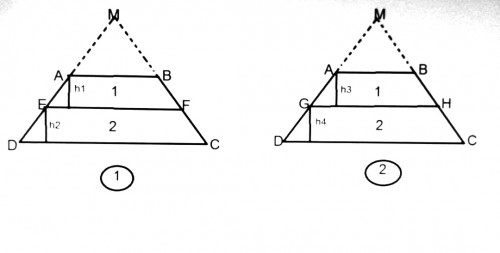
1_در شکل طبق سوال خط EF ذوزنقه رو به تو شکل هم مساحت تبدیل کرده S1=S2 پس :  h1(a+EF)=h2(b+EF)   و    h1/h2=(b+ EF)/(a+EF)

2_از طرفی MEF با MAB متشابه است                                                  

a√3/(2h1+a√3)=a/EF  پس  h1=√3(EF-a)/2

3_حالا از رابطه ای که در بخش اول بدست اومده h2  رو پیدا می‌کنیم         

h2=√3(EF×EF-a×a)/2(b+EF)

4_ حالا سراغ شکل دوم میریم که طبق سوال S1 و S2متشابه هستند          

a/GH=h3/h4   پس   a×h4=GH×h3

5_دوباره میدونیم که MAB و MGH  متشابه هستند                                  

a√3/ ( 2h3+a√3)=a/GH  پس  h3=√3(GH-a)/2

6_ حالا h3 رو تو رابطه بدست اومده در بخش 4 قرار میدیم برای جواب h4 

h4=√3(GH-a)/2 ×GH/a

7_ از طرفی میدونیم h1+h2=h3+h4                                                     

Gh×GH=a×EF + a(EF×EF - a×a)/( b+EF)

Answer 2

• فرض می کنیم. EF=c و GH=d
  
• حالت تشابه. نسبت اضلاع متناظر مناسبند از جمله قاعده ها $$ \frac{a}{d} = \frac{d}{b} \Rightarrow d= \sqrt{ab} $$ در واقع d واسطه هندسی دو قاعده ذوزنقه است
• حالت هممساحت. ارتفاع دو قاعده در دو ذوزنقه بالا و پایین به ترتیب h و k می گیریم $$2S_1=2S_2= S\Rightarrow h(a+c) =k(c+b) = \frac{(a+b)(h+k)}{2} $$ با حل دو معادله دو مجهولی می توانید به جواب زیر برسید $$c= \sqrt{ \frac{a^2 +b^2 }{2 } } $$ در واقع c میانگین مربعی دو قاعده ذوزنقه است.
• رابطه بین آنها نامساوی مهم زیر است $$ \sqrt{ab} \leq \sqrt{ \frac{a^2 +b^2 }{2 } } $$ حتی می توان نشان دا د میانگین حسابی بین میانگین هندسی و مربعی است. یعنی نامساوی زیر داریم $$ \sqrt{ab} \leq \frac{a+b}{2} \leq \sqrt{ \frac{a^2 +b^2 }{2 } } $$