بنام خدا. طبق شکل داریم:
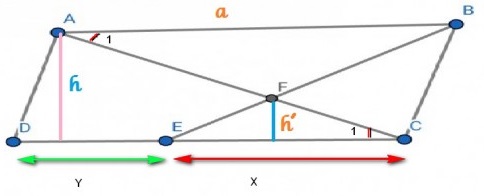
دو مثلث FBA و FEC به حالت دو زاویه متشابهند در راس F متقابل به راس و زاویههای $A$ و $C$ متبادل داخلی. اگر مساحت مثلث FBA را S و مساحت مثلث FEC را $S'$ نشان دهیم باتوجه به اینکه نسبت مساحت دو مثلث متشابه با مجذور نسبت تشابه برابر است خواهیم داشت؛
\begin{align}
& \frac{S}{ S' } = \frac{ a^{2} }{ x^{2} } \Rightarrow \frac{a(h- h' )}{9} = \frac{ a^{2} }{x ^{2} }\\
& \frac{ah-a h' }{9' } = \frac{ a^{2} }{x ^{2} } \Rightarrow \frac{40-a h' }{9} =\frac{ a^{2} }{x ^{2} }
\end{align}
مساحت متوازی الاضلاع دو برابر مساحت مثلث ADC میباشد و
$$ x h' =18\Rightarrow h' = \frac{18}{x} $$
اگراین مقدار را در معادله بالا جایگذاری و سپس معادله را طرفین وسطین کنیم داریم:
\begin{align}
& \frac{40- \frac{18a}{x} }{9} = \frac{ a^{2} }{ x^{2} } \Rightarrow 40 x^{2}-18ax-9 a^{2} =0\\
& x= \frac{9a \pm \sqrt{81 a^{2}+360 a^{2} } }{40} = \frac{3a}{4}
\end{align}
جواب منفی غیرقابل قبول است چون اندازه یک پارهخط همیشه مثبت است. همچنین مجموع X وY مساوی a میباشد یعنی $Y= \frac{a}{4} $ در نتیجه داریم:
$$\frac{X}{Y} = \frac{CE}{DE} = \frac{ \frac{3a}{4} }{ \frac{a}{4} } =\frac{3}{1}=3$$