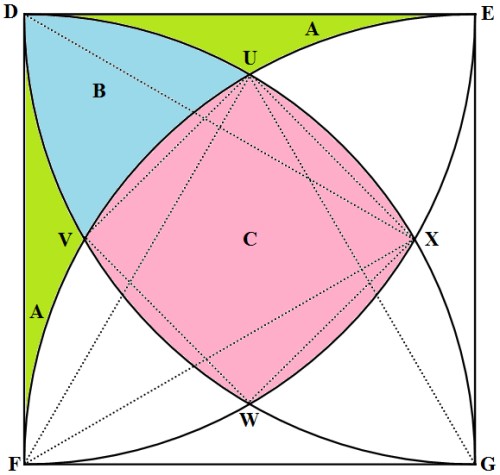
با درود به همه همراهان و اساتید گرامی. با مطالب خوبی که استادان بزرگوار در سؤال مشابه نوشته اند، متوجه شدم که راه حل جبری بنده خطای محاسباتی دارد و قابل ارائه نیست. ولی راه حل جایگزین خود را به اشتراک میگذارم و امیدوارم مفید واقع شود. با توجه به شکل و اینکه مساحت مربع $DEGF$ برابر $1$ است، روابط مستقل زیر قابل استنتاج است.
$I)2A + B = 1 - \frac{\pi }{4}$
$II)2B + C = 1 - 2(1 - \frac{\pi }{4})$
روابط زیر نیز از دو رابطه فوق قابل استنتاج است. ولی چون وابسته به روابط فوق هستند، سودی برای حل مسئله از طریق جبر به تنهایی ندارند. ولی برای حل راحت تر مسئله کمک میکنند.
$III)C - 4A = \pi - 3$
$IV)2A + 3B + C = \frac{\pi }{4}$
$V)4A + 4B + C = 1$
عملاً با دو معادله سه مجهولی روبرو هستیم که بدون شکل کمکی نمیتوان آنرا حل کرد. بنابراین با کمک شکل فوق ادامه میدهیم. چون رئوس چهارضلعی $UVWX$ به اندازه مساوی از میانه اضلاع مربع $DEGF$ جدا شده اند، چهارضلعی فرضی ما مربع است. از طرف دیگر مثلث $ \triangle UFG$ متساوی الاضلاع است، زیرا هردو ساق آن مساوی شعاع دایره و ضلع $ \overline{FG} $ هستند. بنابراین زاویه $ \angle UFG=60^°$ و زاویه $ \angle DFU=30^°$ است. به همین ترتیب با مثلث فرضی $ \triangle DXF$ میتوان ثابت کرد که زاویه $ \angle DFX=60^°$ و زاویه $ \angle XFG=30^°$ است. بنابراین زاویه $ \angle UFX=30^°$ است. حال بکمک زاویه $ \angle UFX=30^°$ و روابط زیر میتوان مساحت مربع فرضی داخلی و قطاعهای دایره اطراف آنرا محاسبه کرد.
$\overline{UX}=2Rsin \frac{ \theta }{2}=2×1×sin15^°= \frac{ \sqrt{6}-\sqrt{2} }{2} $
$S_{ \Box UVWX}=( \frac{ \sqrt{6}-\sqrt{2} }{2} )^2=2- \sqrt{3} $
برای مساحت قطاع با کمان ${UX}$ داریم.
$\Rightarrow S_{U X}=\frac{R^{2}}{2}\left(\frac{\pi \alpha}{180}-\sin \alpha\right)=\frac{1}{2}\left(\frac{30 \pi}{180}-\frac{1}{2}\right)=\frac{\pi-3}{12}$
چون ناحیه بنفش $C$ مجموع چهار قطاع $UX$ باضافه مستطیل داخلی آنهاست، داریم:
$C = 4\frac{{\pi - 3}}{{12}} + 2 - \sqrt 3 = \frac{\pi }{3} - \sqrt 3 + 1$
حال با کمک رابطه (III داریم :
$C - 4A = \pi - 3 \Rightarrow \frac{\pi }{3} - \sqrt 3 + 1 - 4A = \pi - 3 \Rightarrow A = 1 - \frac{{\sqrt 3 }}{4} - \frac{\pi }{6}$
با استفاده از رابطه (I داریم :
$2A + B = 1 - \frac{\pi }{4} \Rightarrow 2\left( {1 - \frac{{\sqrt 3 }}{4} - \frac{\pi }{6}} \right) + B = 1 - \frac{\pi }{4} \Rightarrow B = \frac{\pi }{{12}} + \frac{{\sqrt 3 }}{2} - 1$
برای آزمون صحت یافته هایمان میتوانیم از رابطه (V استفاده کنیم.
$ 4\left( {1 - \frac{{\sqrt 3 }}{4} - \frac{\pi }{6}} \right) +4\left( {\frac{\pi }{{12}} + \frac{{\sqrt 3 }}{2} - 1} \right) + \frac{\pi }{3} - \sqrt 3 + 1 = 1$
حال رابطه های درخواستی سؤال بترتیب زیر بدست می آید.
$\frac{A}{B} = \frac{{1 - \frac{{\sqrt 3 }}{4} - \frac{\pi }{6}}}{{\frac{\pi }{{12}} + \frac{{\sqrt 3 }}{2} - 1}} = \frac{{9\sqrt 3 - 12}}{{\pi + 6\sqrt 3 - 12}} - 2 \approx {\rm{0}}{\rm{.33943745944704906}}$
$\frac{A}{C} = \frac{{1 - \frac{{\sqrt 3 }}{4} - \frac{\pi }{6}}}{{\frac{\pi }{3} - \sqrt 3 + 1}} = \frac{{18 - 9\sqrt 3 }}{{4(\pi - 3\sqrt 3 + 3)}} - \frac{1}{2} \approx {\rm{0}}{\rm{.13767720399083794}}$
$\frac{B}{C} = \frac{{\frac{\pi }{{12}} + \frac{{\sqrt 3 }}{2} - 1}}{{\frac{\pi }{3} - \sqrt 3 + 1}} = \frac{{9\sqrt 3 - 15}}{{4(\pi - 3\sqrt 3 + 3)}} + \frac{1}{4} \approx {\rm{0}}{\rm{.4056040373832518}}$
طبیعی است اگر واحد ما بزرگتر از $1$ و مساوی $n$ باشد، همه مساحتهای بدست آمده به ${n^2}$ ضرب میشوند ولی نسبت مساحتها بهم ثابت میماند. با آرزوی تندرستی و سرافرازی برای یکایک همراهان و استادان گرامی که مطالب خوبشان همیشه الهام بخش بنده بوده.