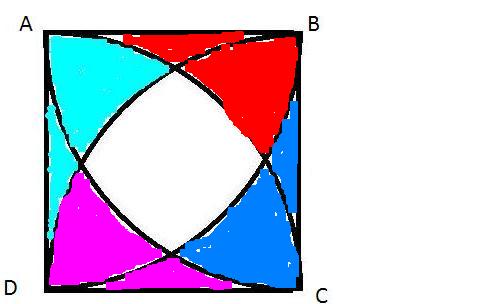
ШЁШұШ§ЫҢ ШЁШҜШіШӘ ШўЩҲШұШҜЩҶ Щ…ШіШ§ШӯШӘ Щ…ШұШ§ШӯЩ„ ШІЫҢШұ ШұШ§ Ш§ЩҶШ¬Ш§Щ… Щ…ЫҢ ШҜЩҮЫҢЩ…:
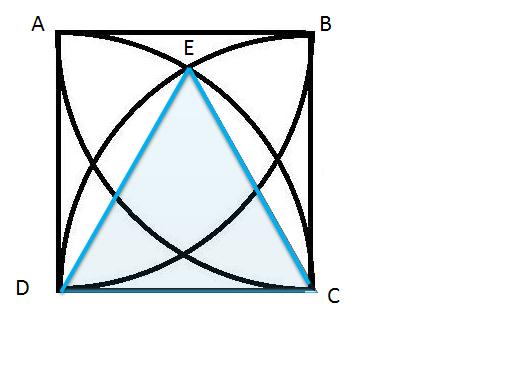
Ш§ШІ ЩҶЩӮШ·ЩҮ ЫҢ $ E $ ШЁЩҮ ЩҶЩӮШ§Ш· $ C $ ЩҲ $ D $ ЩҲШөЩ„ Щ…ЫҢЪ©ЩҶЫҢЩ… ШӘШ§ Щ…Ш«Щ„Ш« Щ…ШӘШіШ§ЩҲЫҢ Ш§Щ„Ш§Ш¶Щ„Ш§Ш№ ШЁЩҮ Щ…ШіШ§ШӯШӘ $ \frac{100 \sqrt{3} }{4} $ ШЁШҜШіШӘ ШўЫҢШҜ.
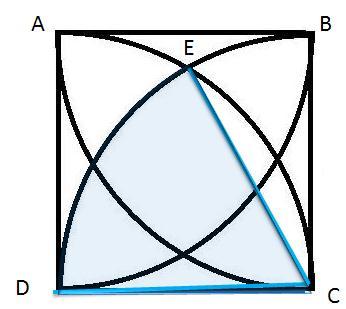
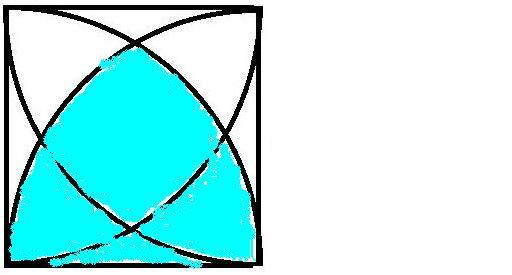
ЩҶШ§ШӯЫҢЩҮ ЫҢ ШұЩҶЪҜЫҢ ШҜШұ ШҙЪ©Щ„ ШЁШ§Щ„Ш§ ЩӮШ·Ш§Ш№ЫҢ Ш§ШІ ШҜШ§ЫҢШұЩҮ ШЁЩҮ ШІШ§ЩҲЫҢЩҮ ЫҢ 60 Ш§ШіШӘ Ъ©ЩҮ Щ…ШіШ§ШӯШӘ ШўЩҶ ШЁШұШ§ШЁШұ Ш§ШіШӘ ШЁШ§ $ \frac{100 \pi}{6} $
ШЁШ§ Щ…ЩҶЩҮШ§ Ъ©ШұШҜЩҶ Щ…ШіШ§ШӯШӘ ЩҮШ§ЫҢ ШЁШҜШіШӘ ШўЩ…ШҜЩҮ Щ…ШіШ§ШӯШӘ ЩҶШ§ШӯЫҢЩҮ ЫҢ ШұЩҶЪҜЫҢ ШІЫҢШұ ШЁШҜШіШӘ Щ…ЫҢ ШўЫҢШҜ Ъ©ЩҮ ШЁШұШ§ШЁШұ Ш§ШіШӘ ШЁШ§
$ \frac{100 \pi}{6} - \frac{100 \sqrt{3} }{4}$
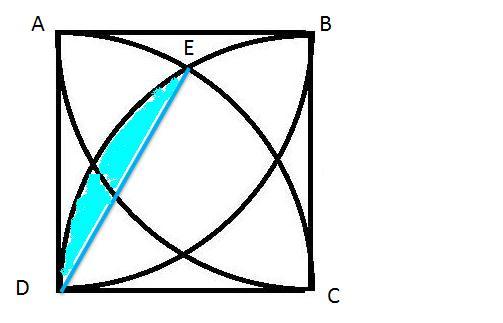
ШЁШ§ ШҜЩҲ ШЁШұШ§ШЁШұ Ъ©ШұШҜЩҶ ШўЩҶ ЩҲ Ш¬Щ…Ш№ ШЁШ§ Щ…ШіШ§ШӯШӘ Щ…Ш«Щ„Ш« Щ…ШіШ§ШӯШӘ ЩҶШ§ШӯЫҢЩҮ ЫҢ ШІЫҢШұ ШЁШҜШіШӘ Щ…ЫҢ ШўЫҢШҜ.
$ \frac{100 \pi}{3} - \frac{100 \sqrt{3} }{2}+ \frac{100 \sqrt{3} }{4}= \frac{100 \pi}{3} - \frac{100 \sqrt{3} }{4}$
ШӯШ§Щ„ Ш§ЪҜШұ ШұШЁШ№ ШҜШ§ЫҢШұЩҮ ШЁШ§ Ъ©Щ…Ш§ЩҶ $AEC$ ШұШ§ ШҜШұ ЩҶШёШұ ШЁЪҜЫҢШұЫҢЩ… Щ…ШіШ§ШӯШӘ ШўЩҶ ШЁШұШ§ШЁШұ Ш§ШіШӘ ШЁШ§ $\frac{100 \pi}{4}$ ЩҲ Ш§ЪҜШұ Ш§ШІ ШўЩҶ ЩҶШ§ШӯЫҢЩҮ ЫҢ ШұЩҶЪҜЫҢ ШЁШ§Щ„Ш§ ШұШ§ Ъ©Щ… Ъ©ЩҶЫҢЩ… Щ…ШіШ§ШӯШӘ ЩҶШ§ШӯЫҢЩҮ ЫҢ ШұЩҶЪҜЫҢ
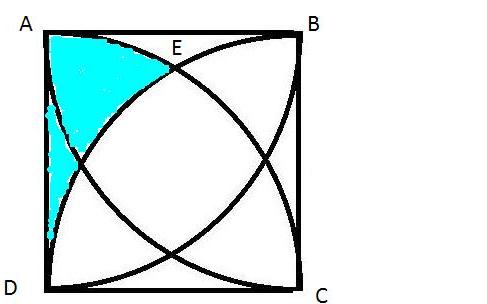
ШЁШҜШіШӘ Щ…ЫҢ ШўЫҢШҜ Ъ©ЩҮ ШЁШұШ§ШЁШұ Ш§ШіШӘ ШЁШ§:
$\frac{100 \pi}{4}- \frac{100 \pi}{3} + \frac{100 \sqrt{3} }{4}=\frac{100 \pi}{12}+ \frac{100 \sqrt{3} }{4}$
ШӯШ§Щ„ Ш§ЪҜШұ ШҜЩӮШӘ Ъ©ЩҶЫҢЩ… ЩҶШ§ШӯЫҢЩҮ Ш®ЩҲШ§ШіШӘЩҮ ШҙШҜЩҮ ШЁШұШ§ШЁШұ Щ…ШӘЩ…Щ… 4 ШЁШұШ§ШЁШұ ЩҶШ§ШӯЫҢЩҮ ЫҢ ШЁШ§Щ„Ш§ Ш§ШіШӘ ЪҶЩҲЩҶ: