ШЁШұШ§ЫҢ ШіШ§ШҜЩҮ ШЁЩҲШҜЩҶ Щ…ШӯШ§ШіШЁШ§ШӘ ЩҒШұШ¶ Ъ©ЩҶЫҢЩ… Ш¶Щ„Ш№ Щ…ШұШЁШ№ ШЁШұШ§ШЁШұ $2$ Ш§ШіШӘ ЩҲ ШҜШұ ШўШ®Шұ Ш¬ЩҲШ§ШЁ ШұШ§ ШҜШұ $\frac{a}{4}$ Ш¶ШұШЁ Щ…ЫҢЪ©ЩҶЫҢЩ… ШӘШ§ ШЁШұШӯШіШЁ $a$ ШЁШҜШіШӘ ШўЫҢШҜ
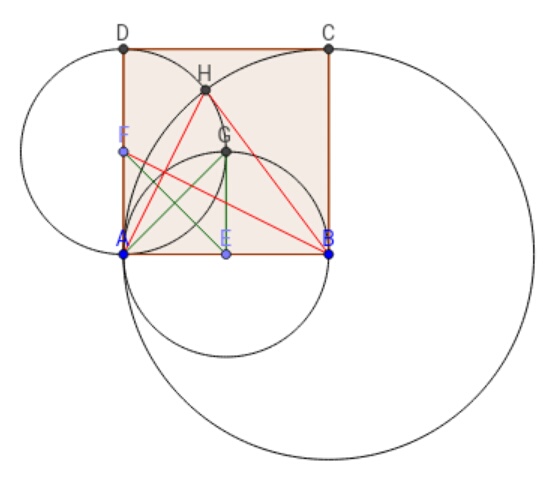
Ш§ШЁШӘШҜШ§ ШҜЩҲ ЩҲШӘШұ Щ…ШҙШӘШұЪ© ШұШ§ ШұШіЩ… Ъ©ШұШҜЩҮ ЩҲ Щ…ШұЪ©ШІ ШҜШ§ЫҢШұЩҮ ЩҮШ§ ШұШ§ ШЁЩҮЩ… ЩҲШөЩ„ Щ…ЫҢЪ©ЩҶЫҢЩ…
ШҙШ№Ш§Ш№ ШҜШ§ЫҢШұЩҮ ЩҮШ§ЫҢ Ъ©ЩҲЪҶЪ© ШЁШұШ§ШЁШұ $1$ ЩҲ ШҜШ§ЫҢШұЩҮ ШЁШІШұЪҜ ШЁШұШ§ШЁШұ $2$ Щ…ЫҢШЁШ§ШҙШҜ
Щ…ШіШ§ШӯШӘ ЩӮШіЩ…ШӘ Щ…ШҙШӘШұЪ© ШҜЩҲ ШҜШ§ЫҢШұЩҮ Ъ©ЩҲЪҶЪ©:
$$S_{AG}=2(\pi AF^2 \frac{90}{360}-\frac{1}{2}AF^2) \approx 0.6$$
$$sin(AFB)=\frac{2}{ \sqrt{5}} \Rightarrow \\Arcsin(\frac{2\sqrt{5}}{5}) \approx 63.4 \\ \Rightarrow \hat{AFH}=126.8 $$
$$sin(ABF)=\frac{1}{\sqrt{5}} \Rightarrow \\Arcsin(\frac{\sqrt{5}}{5}) \approx 26.6 \\ \Rightarrow \hat{ABH} =53.2$$
Щ…ШӯШ§ШіШЁЩҮ Щ…ШіШ§ШӯШӘ ЩӮШ·Ш№ЩҮ ШЁЫҢЩҶ $AH$ ЩҲ Ъ©Щ…Ш§ЩҶ ШҜШ§ЫҢШұЩҮ ШЁШІШұЪҜ:
$$S_{1}=(\pi AB^2 \times \frac{53.2}{360})- (\frac{1}{2} AB^2 sin(ABH)) \approx 0.3$$
Щ…ШӯШ§ШіШЁЩҮ Щ…ШіШ§ШӯШӘ ЩӮШ·Ш№ЩҮ ШЁЫҢЩҶ $AH$ ЩҲ Ъ©Щ…Ш§ЩҶ ШҜШ§ЫҢШұЩҮ Ъ©ЩҲЪҶЪ©:
$$S_{2}=(\pi AF^2 \times \frac{126.8}{360})- (\frac{1}{2} AF^2 sin(AFH) \approx 0.7$$
ШӯШ§Щ„ Ш§ШІ Ш¬Щ…Ш№ Ш§ЫҢЩҶ ШҜЩҲ Щ…ШіШ§ШӯШӘ Щ…ШҙШӘШұЪ© ШЁЫҢЩҶ ШҜШ§ЫҢШұЩҮ ШЁШІШұЪҜ ЩҲ Ъ©ЩҲЪҶЪ© ШұЩҲЫҢ ЩҲШӘШұ $AH$ ШЁШҜШіШӘ Щ…ЫҢ ШўЫҢШҜ:
$$S_{AH}=S_{1}+S_{2}=0.3+0.7=1$$
$$S_{AH}-S_{AG}=1-0.6=0.4$$
Ш§ЪҜШұ Ш¶Щ„Ш№ Щ…ШұШЁШ№ $2$ ШЁШ§ШҙШҜ Щ…ШіШ§ШӯШӘ ЩӮШіЩ…ШӘ ШұЩҶЪҜЫҢ ШЁШұШ§ШЁШұ $0.4$ Щ…ЫҢШЁШ§ШҙШҜ
ЩҲШ§ЪҜШұ Ш¶Щ„Ш№ Щ…ШұШЁШ№ $a$ ШЁШ§ШҙШҜ Щ…ШіШ§ШӯШӘ ЩӮШіЩ…ШӘ ШұЩҶЪҜЫҢ ШЁШұШ§ШЁШұ $0.1 \times a$ Щ…ЫҢШҙЩҲШҜ.