مساحت خواسته شده به صورت زیر محاسبه می شود:
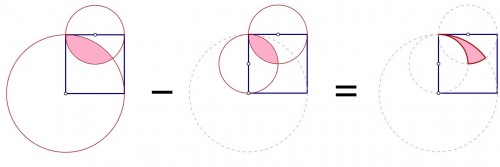
هر یک از قسمت های اول و دوم اشتراک دو دایره هستند. که به آن لنز(lens) گفته می شود. نحوه محاسبه یکی از آنها را انجام می دهم. دیگری به طور مشابه بدست می آید.
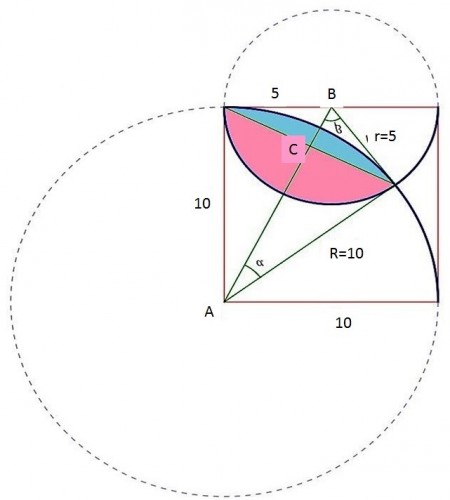
از روابط بین مثلثهای قائم الزاویه داریم:
$$AC.AB=R^2 \rightarrow AC= \frac{R^2}{AB}= \frac{100}{ \sqrt{125} } $$
حال داریم:
$$cos( \alpha )= \frac{AC}{R}= \frac{10}{ \sqrt{125}}=0.894427191 $$
پس زاویه $ \alpha $ برابر $26.5650511771 $ است. همچنین داریم که $ \beta =90- \alpha =90-26.5650511771=63.4349488229$
طبق رابطه ایی که برای (lens) آمده مساحت ناحیه آبی برابر است با:
$$ \frac{1}{2}R^2( 2\alpha _{radian}-sin(2 \alpha_{degree} ))=50(0.9268251188-0.8)=6.34125594 $$
همچنین مساحت ناحیه صورتی برابر است با:
$$ \frac{1}{2}r^2( 2 \beta _{radian}-sin(2 \beta ))=12.5(2.2131748812-0.8)=17.6646860144 $$
احتمال اشتباه محاسباتی وجود دارد.