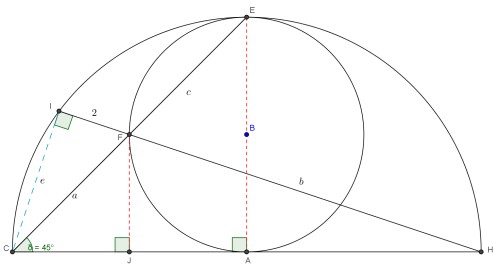
چون زاویه $FCA$ ،45 درجه است پس: $ 45^{ \circ }= \frac{ 180^{\circ}- FAکمان} {2} $
لذا کمان $FA$ ، 90 درجه است و اگر از نقطه $F$ بر $CH$ عمود کنیم $FJ=CJ=R$ و به این ترتیب شعاع نیم دایره $2R$ و شعایع دایره محاطی در شکل برابر $R$ خواهد بود .باتوجه به تالس $FC=FE=a$ و با توجه به دو وتر متقاطع $2b=a^{2}$ وازطرفی $a^{2}=2R^{2}$ .
در مثلث های قائم الزاویه $CIH$و$CIF$ :
$ a^{2}-4=16R^{2}-(b+2)^{2} $
$ 2R^{2}-4=16R^{2}-(R^{2}+2)^{2} \Rightarrow R^{4}-10R^{2}=0 \Rightarrow R= \sqrt{10} $
درنتیجه مساحت مثلث $FCH$برابر است با:
$\color{red}{ \frac{1}{2} \times \sqrt{10} \times 4\sqrt{10}=20} $