چهار نقطه روی دایره،دایره را به چهار کمان مساوی تقسیم کرده اند مساحت قسمت رنگی چقدر است ؟

Question

در شکل زیر چهار نقطه روی دایره،دایره را به چهار کمان مساوی تقسیم کرده اند.به مرکز هر یک از این چهار نقطه چهار کمان رسم کرده ایم .مساحت قسمت رنگی حاصل از برخورد چهار کمان را بدست آورید.

Comments

@math
سلام
عذر میخوام اما سوال شما با سوال من فرق نداره فقط  مربع در سوال من (http://math.irancircle.com/5876/)
به دایره ای تبدیل شده که قطر آندو برابرند و باعث ایجاد 4 هلال شده که در خواسته سوال تغییری ایجاد نمیکنه .

---

سلام
بله حق با شماست ، اما حل این سوال برای من خیلی سخت بود، چون من نمونه همین سوال رو در جای دیگه دیدم که با انتگرال حل کرده بود من دنبال راه دیگه ای برای حل اینطور مسائل بودم.
که fardina عزیز لطف کردن و وقت گذاشتن.
ممنونم

Answer 1

اگر چهار نقطه روی دایره را به هم وصل کنید یک مربع تشکیل می شود:

در اینصورت این سوال شبیه به سوال موجود در اینجا هست: مساحت قسمت رنگی( شکل از برخورد 4 ربع دایره حاصل شده است) چقدر است ؟

---

درحالت کلی فرض کنید طول ضلع مربع $a$ باشد.

در اینصورت با توجه به شکل زیر

مساحت مثلثی که با رنگ صورتی نشان داده شده است برابر است با

$$S_1=\frac{\sqrt{3}}4a^2$$ (چون یک مثلث متساوی الاضلاع به ضلع $a$ است)

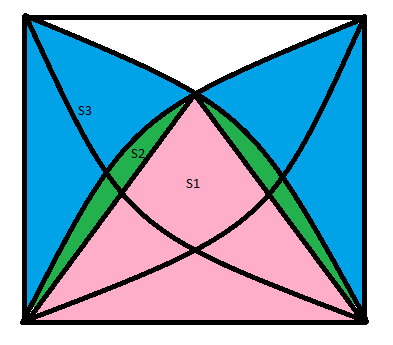
چون $S_2$ کمان روبروی به زاویه ی $60^\circ$ است لذا مساحت آن برابر است با

$$S_2=\frac{\pi a^2}{6}-S_1=\frac{\pi a^2}{6}-\frac{\sqrt 3}4a^2$$

همچنین $S_2+S_3$ برابر با مساحت قطاعی از دایره است که با زاویه $30^\circ$ جدا شده است پس

$$S_2+S_3=\frac{\pi a^2}{12}$$ بنابراین $$S_3=\frac{\pi a^2}{12}-S_2=\frac{\pi a^2}{12}-\frac{\pi a^2}{6}+\frac{\sqrt 3}4a^2$$

بنابر تقارن موجود مساحت قسمت رنگی که مد نظر شما هست برابر است با مساحت مربع منهای چهار تا مساحت $S_3$

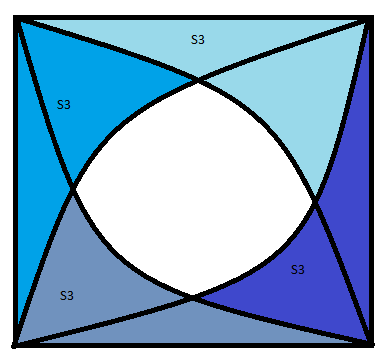
بنابراین

$$S=S_{square}-4S_3=a^2-4(\frac{\pi a^2}{12}-\frac{\pi a^2}{6}+\frac{\sqrt 3}4a^2)$$