دو مثلث $ OBM $ و $ OAD$ متشابه هستند (چرا؟) پس
$ k= \frac{OA}{OM} = \frac{OD}{OB} = \frac{AD}{BM} =2 $
نسبت مساحت ها برابر است $ K^{2}=4 $ یعنی $ S_{OAD}=4 S_{OBM} $
از اینکه نسبت تشابه برابر $ 2 $ داریم$ OD=2OB$ پس
$S_{OAD}=2 S_{OAB} $ پس $ S_{OAB}=2S_{OBM}$
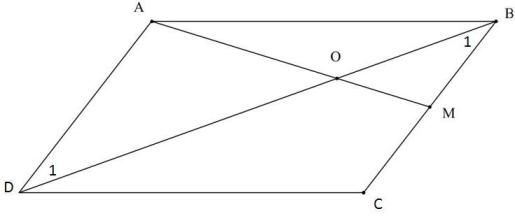
مساحت متوازی الاضلا برابر است با $ 2 S_{ABD} $ لذا داریم:
$ S_{ABCD}=2 S_{ABD}=2( S_{OAB}+S_{OAD})=2(4 S_{OBM}+2S_{OBM})=12S_{OBM}$