برای اینکه منحنی با ضابطهٔ $y=(2x+1)(x+8)$ و خط با ضابطهٔ $y=mx$ برخوردی نداشته باشند، $m$ چه مقداری باید داشته باشد؟

Question

منحنی به معادلهٔ $y=(2x+1)(x+8)$ با خط $y=mx$ نقطهٔ مشترک ندارد. مجموعه‌مقادیرِ ممکن برای $m$ را بدست‌آورید.

Comments

بله درست میفرمایید ... تصحیح میکنم :
منحنی به معادله (y=(2x+1) (x+8 با خط y=mx نقطه مشترک ندارد . مجموعه مقادیر m را بدست آورید

---

پس وقتی طرف های دوم این دو را مساوی هم قرار می دهیم معادله درجه دوم تشکیل شده نباید ریشه داشته باشد یعنی دلتای ان را کوچکترازصفر قرار دهید ونامعادله را حل کنید
امتحان کنید

---

بله متشکرم جواب میشه بازه ی باز 9 و 25

---

خیلی خوب
لطف دارید

Answer 1

از اینکه منحنی‌تان به شکل $y$ برابر با حاصلضرب دو چندجمله‌ایِ درجهٔ یک بر حسب $x$ پس یعنی $y$ برابر با یک چندجمله‌ای درجهٔ دو بر حسب $x$ داده‌شده‌است خیلی راحت باید متوجه شوید که منحنی‌تان یک سهمیِ عمودیِ ساده است. یک شکل از آن رسم کنید، اگر از نرم‌افزار استفاده نمی‌کنید، کافیست چند عدد جایگذاری کنید و چند نقطه از آن را پیدا و سهمی‌وار به هم وصل کنید. مشخص است که این سهمی از مبدأ نمی‌گذرد (چون جمله ثابتِ ناصفر دارد) بعلاوه مبدأ درونِ سهمی قرار نمی‌گیرد. اگر مبدأ درون سهمی قرار می‌گرفت، آنگاه هر خط گذرنده از مبدأ حتما این سهمی را قطع می‌کرد. در زیر یک شکل از این سهمی که با نرم‌افزار Maple کشیده‌شده‌است را می‌بینید.

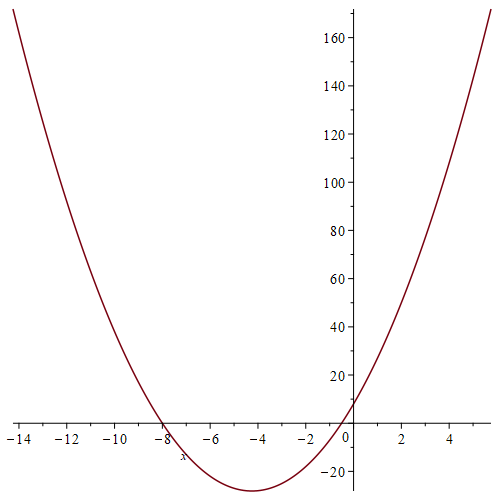
توجه کنید که $y=mx$ها خط‌های گذرنده از مبدأ هستند. یک خط گذرنده از مبدأ که بر سهمی مماس باشد در واقع یکی از مماس‌های کشیده‌شده از مبدأ بر سهمی خواهدبود. پس بیاییم این خط‌ها را بیابیم. چرا؟ چون مرز خط‌هایی که با سهمی برخورد دارند خط‌هایی هستند که بر سهمی مماس هستند (شاید کمی بعد از اینجا برایتان معنای این حرف روشن شود). برای یافتن خط مماس بر سهمی وارد شده از مبدأ کافیست نقطهٔ برخورد این چنین خط با سهمی را بیابیم. آنگاه مبدأ و آن نقطه دو خط از این خط هستند و با داشتن دو نقطه از یک خط، ضابطه و تمام داده‌های خط را داریم. به فرض $A$ یکی از نقطه‌هایی از سهمی باشد که از مبدأ می‌توان خط مماسی بر سهمی رسم کرد که سهمی را در این نقطه لمس می‌کند. در این صورت شیب خط مماس برابر است با $m=\frac{y_A-y_O}{x_A-x_O}$ و همینطور برابر است با $m=y'\mid_{x_A}$. مشتق ضابطهٔ سهمی نسبت به $x$ برابر می‌شود با $4x+17$ پس برابری (معادله) زیر را داریم.

$$4x+17=\frac{(2x+1)(x+8)-0}{x-0}$$

که چون از شکل مشخص است که $x_A\neq 0$ پس می‌توان دو طرف برابری را در $x$ ضرب کرد.

$$4x^2+17x=2x^2+17x+8$$

که با ساده‌سازی دو طرف، یک برابریِ درجهٔ دوی ساده داریم با ریشه‌های $x=\pm 2$. با جایگذاری آنها در ضابطهٔ سهمی داریم .

$$A=(2,50)\text{ یا }A=(-2,-18)$$

پس دو مماس از مبدأ بر این سهمی می‌توان رسم کرد. که با گذاشتن مختصات نقطه‌های لمسی در $y=mx$ به دو مقدارِ $m=25$ و $m=9$ می‌رسیم. در زیر شکل سهمی (به رنگ آبی) و دو خط گذرنده از مبدأ مرتبط با دو مقدارِ یافت‌شده برای $m$ (به رنگ قرمز) را می‌بینید.

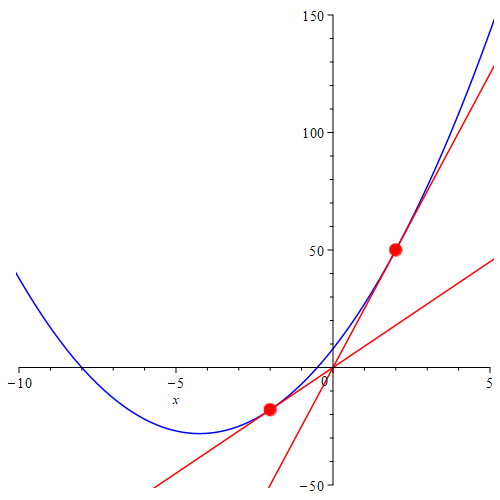
اگر $m$ را از ۲۵ افزایش دهید خط قرمز بالای راستی را دارید که در جهت خلاف عقربه‌های ساعت به سمت محور $y$ها حرکت می‌کند که با سهمی در یک‌چهارمِ یکُم صفحه برخورد دارد. اگر مقدار $m$ را از ۹ کاهش دهید خط قرمز بالای چپ را خواهید داشت که در سمت عقربه‌های ساعت به سمت محور $x$ها و سپس محور $y$ها نزدیک خواهد شد و به ترتیب ابتدا در یک‌چهارمِ سوم و سپس در یک‌چهارمِ دوم صفحه با سهمی برخورد خواهد داشت. اما اگر مقدار $m$ بین ۹ و ۲۵ باشد، آنگاه خط‌تان بین دو خط قرمز رنگ قرار خواهد داشت که سهمی را در هیچ نقطه‌ای قطع نخواهد کرد. پس پاسخی که دنبالش هستید بازهٔ بازِ $m\in (9,25)$ است.