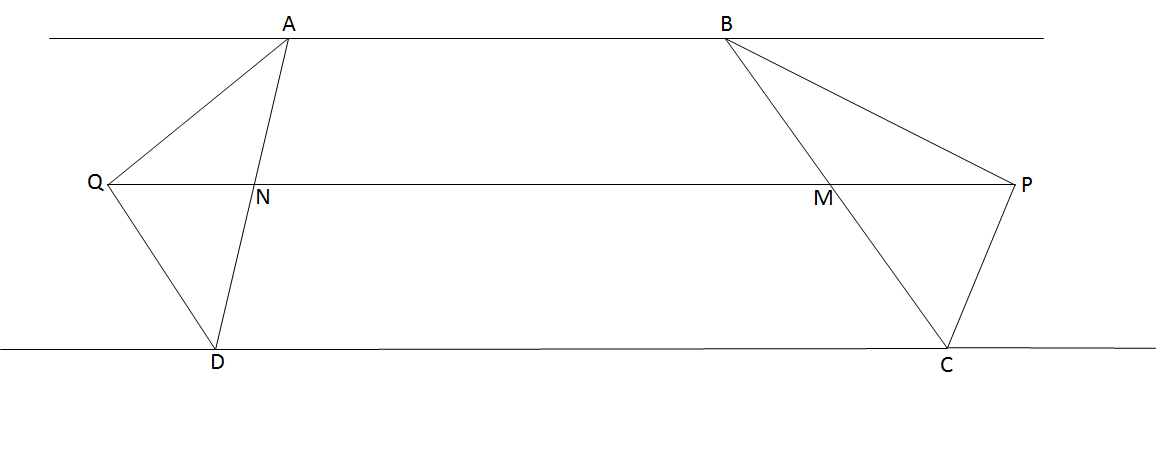
به آسانی ثابت میشود که مثلث های $BPC$ و $AQD$ قائم الزاویه اند. اکنون ثابت میکنیم $M$ و $N$ وسط های دو ساق هستند. عمودهای وارد از $P$ به ترتیب بر $AB$ و $BC$ و $CD$ را $K$ و $H$ و $T$ مینامیم. چون $BP$ نیمساز خارجی $B$ است، پس $PK=PH$ و چون $CP$ نیمساز خارجی $C$ است، پس $PH=PT$. از این دو نتیجه میشود که $PK=PT$ و این یعنی فاصله ی $P$ از $AB$ و $CD$ برابر است. به طریق مشابه اثبات میشود که فاصله ی $Q$ نیز از $AB$ و $CD$ برابر است. بنابراین فاصله ی پاره خط $PQ$ از $AB$ و $CD$ برابر است، پس $M$و $N$ وسط های $BC$ و $AD$ هستند.
چون $M$ و $N$ وسط های $BC$ و $AD$ هستند پس $MN= \frac{AB+CD}{2} $.
میدانیم و میتوان اثبات کرد که میانه ی وارد بر وتر نصف وتر است.پس :
از اینکه مثلث $BPC$ قائم الزاویه است و اینکه $M$ وسط $BC$ است نتیجه میشود $PM= \frac{BC}{2} $.
از اینکه مثلث $AQD$ قائم الزاویه است و اینکه $N$ وسط $AD$ است نتیجه میشود $QN= \frac{AD}{2} $.
بنابراین داریم:
$$PQ=PM+MN+NQ$$
$$= \frac{BC}{2} + \frac{AB+CD}{2} + \frac{AD}{2} $$
$$= \frac{AB+BC+CD+DA}{2} $$
پس حکم اثبات شد.