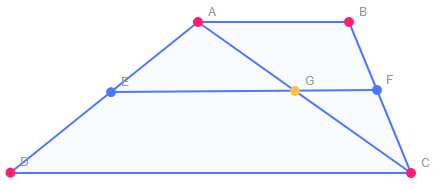
ابتدا ثابت میکنیم که موازی اند برای این کار $E$ را وسط ساق $AD$ در نظر میگیریم و از نقطه $E$ خطی به موازات قاعده ها رسم میکنیم تا ساق $BC$ را در نقطه $F$ قطع کند و نشان میدهیم که $F$ وسط $BC$ است.
$EG \parallel DC \Rightarrow \frac{AG}{GC}= \frac{AE}{ED}
\Rightarrow \frac{AG}{GC}=1 $
$GF \parallel AB \Rightarrow \frac{BF}{FC}= \frac{AG}{GC}
\Rightarrow\frac{BF}{FC}=1 \Rightarrow BF=FC $
پس ثابت شد که موازی اند.حالا ثابت میکنیم که طول $EF$ برابر است با میانگین حسابی دو قاعده(با توجه به قضیه تالس و تشابه).
$EG \parallel DC \Rightarrow \bigtriangleup AEG \sim \bigtriangleup ADC \Rightarrow EG=\frac{1}{2}DC $
$GF \parallel AB \Rightarrow \bigtriangleup GFC \sim \bigtriangleup ABC \Rightarrow GF=\frac{1}{2}AB$
و با جمع کردن طرفین این دو رابطه بالا داریم:
$EG+GF=EF=\frac{1}{2}(AB+DC)$
و ثابت میشود...