طول خط موازی با قاعده که ذوزنقه را دو نیم میکتد

Question

سلام وقت بخیر این فرمول تو کنکور سال ۹۹ اومده بود: طول خط موازی با قاعده ذوزنقه که مساحتش را دو نیم میکند برابر است با: $ \sqrt{ \frac{ x^{2}+ y^{2} }{2} } $

متغیر های x و y همون قاعده های ذوزنقه هستن. میشه اثباتش کنین بی زحمت؟

Answer 1

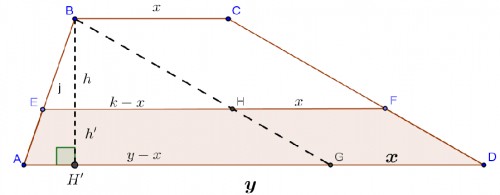
باتوجه به شکل BG را موازی CD رسم می کنیم.باتوجه به تساوی مساحت ها

$ h(k+x)=h'(k+y) \Rightarrow \frac{h}{h'}=\frac{k+y}{k+x} $

وبا توجه تشابه مثلث ها $ \frac{k-x}{y-x}= \frac{h}{BH'} \Rightarrow \frac{k-x}{y-k}= \frac{h}{h'} $

از دو تساوی فوق خواهیم داشت:

$\frac{k-x}{y-k}=\frac{k+y}{k+x}\Rightarrow y^2-k^2=k^2-x^2\Rightarrow k^2= \frac{x^2+y^2}{2}\Rightarrow EF=k= \sqrt{\frac{x^2+y^2}{2}} $

Comments

خیلی ممنون از شما دوست دانشمند

---

@Amin rezaeeyan متشکرم. البته من دانشمند نیستم دبیری باتجربه هستم که علاقه خاصی به ریاضی و حل مسائل آن دارم.

---

خیلی ممنون
فقط عذر میخوام میشه اون قسمت تعمیم تالس رو بگین چجوری اومد؟
من اصلا متوجه نشدم
مخصوصا y منهای k کجای مثلث میشه که ازش تو تالس استفاده شده؟

---

@Amin rezaeeyan اصلاح کردم تشابه مثلثها، مثلث BEH و BAG به حالت داشتن دو زاویه مساوی متشابهند و نسبت تشابه اضلاع با نسبت ارتفاع های نظیر برابرند.
با توجه به خواص تناسب از خاصیت تفضیل صورت در مخرج نسبت ها پدید آمده است. مقدار صورت ها از مخرج ها کسر کردم

---

ممنون که وقت گذاشتین
خیلی ممنون