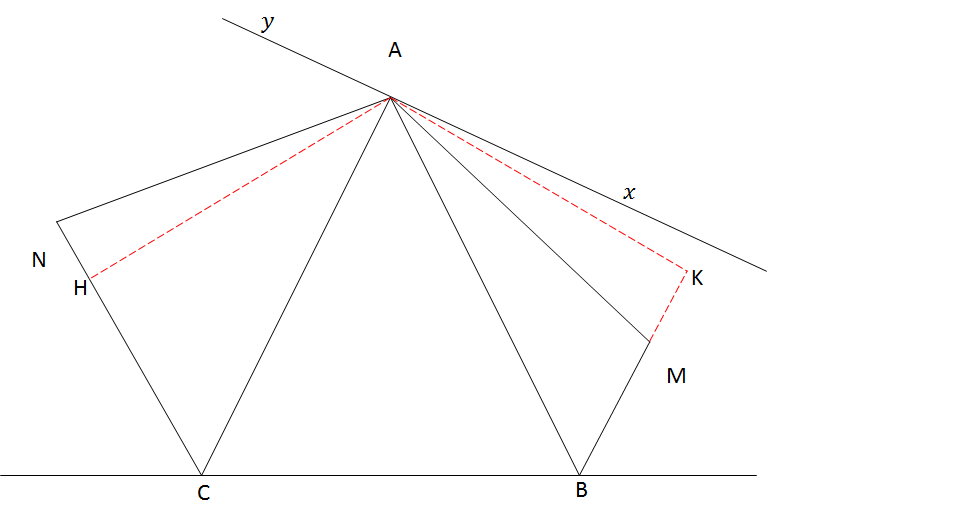
ابتدا توجه کنید که $ \hat{BAC} = \hat{ABM} =60$ پس $AC$ و $BM$ موازی اند به طریق مشابه ثابت میشود $CN$ و $AB$ هم موازی اند.
اکنون ثابت میکنیم $ \hat{CAM} + \hat{BAN} =180$. به این منظور داریم:
$$ \hat{CAM} + \hat{BAN} $$
$$=( \hat{CAB} + \hat{BAM} )+( \hat{BAC} + \hat{CAN} )$$
$$=120+ \hat{BAM} + \hat{CAN} $$
$$=120+ \frac{ \hat{CAy} }{2} + \frac{ \hat{BAx} }{2} $$
$$=120+( \frac{180- \hat{BAC} }{2} )$$
$$=120+ \frac{180-60}{2} $$
$$=180$$
پس ثابت شد که $ \hat{CAM} + \hat{BAN} =180$. از اینکه $BM$ موازی $AC$ است نتیجه میشود $ \hat{AMB} + \hat{CAM} =180$ و از اینکه $CN$ موازی $AB$ است نتیجه میشود $ \hat{CNA} + \hat{BAM} =180$. پس داریم:
$$ \hat{BMA} + \hat{CNA} $$
$$=(180- \hat{CAM} )+(180- \hat{BAN} )$$
$$=360-( \hat{BAN} + \hat{CAM} )$$
$$=360-180$$
$$=180$$
پس $ \hat{BMA} $ و $ \hat{CNA} $ مکمل هم هستند و همچنین $ \hat{BMA} $ و $ \hat{AMK} $ هم مکمل هم هستند درنتیجه $ \hat{CNA} = \hat{AMK} $.
عمود های وارد از $A$ بر $BM$ و $CN$ را به ترتیب $K$ و $H$ مینامیم. در دو مثلث $BAK$ و $CAH$ داریم $AB=AC$ و $ \hat{ABK} = \hat{ACH} =60$. پس دو مثلث به حالت وتر و زاویه ی تند هم نهشتند بنابراین $AK=AH$.
اکنون در دو مثلث $AMK$ و $ANH$ چون $ \hat{AKM} = \hat{AHN} =90$ و $ \hat{ANH} = \hat{AMK} $ نتیجه میشود $ \hat{MAK} = \hat{NAH} $ اکنون داریم $AK=AH$ و $ \hat{AKM} = \hat{AHN} =90$ و $ \hat{NAH} = \hat{MAK} $ پس دو مثلث به حالت ز.ض.ز هم نهشت اند. بنابراین:
$$AM=AN$$
حکم ثابت شد.