چون در هندسه هذلولی ما قادر به نمایش عدد $\pi$ روی خط راست در این محیط میباشیم که این خط راست میتواند در هندسه اقلیدسی یک خم باشد.
ولی در هندسه اقلیدسی درست است که در محیط دایره میتوان $\pi$ را نمایش دهیم ولی نمایش آن روی خط راست این محیط ممکن نیست.
حال اگر $\pi$ را در خط راست داشته باشیم به شکل زیر توجه کنید:
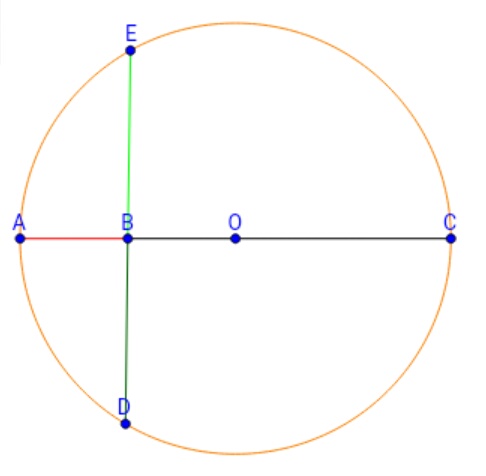
$$AB \times BC=BD \times BE$$
وتر بر قطر عمود است و به دوقسمت مساوی تقسیم شده و قسمتی از قطر که قرمز است به اندازه یک واحد است
حال فرض کنید خط سیاه به اندازه $\pi$ باشد آنگاه $BD=BE$ و آن هم برابر جذر $\pi$ یا ضلع مربع به مساحت $\pi$ میباشد.
$$BD=BE= \sqrt{BC}=\sqrt{\pi}$$