Ш·ШЁЩӮ ШҙЪ©Щ„ ШІЫҢШұШҢ
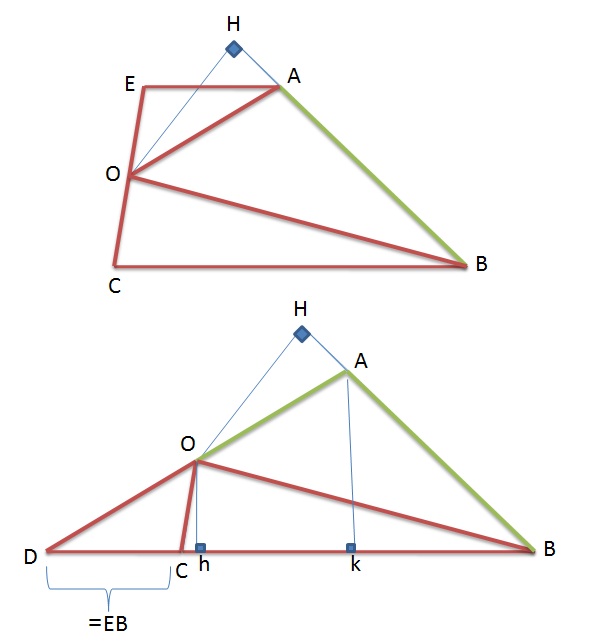 Щ…ЫҢ Ш®ЩҲШ§ЩҮЫҢЩ… Ш«Ш§ШЁШӘ Ъ©ЩҶЫҢЩ…:
$$ S_{EACB}=OH.AB $$
ШЁШ§ ШӘЩҲШ¬ЩҮ ШЁЩҮ ШҙЪ©Щ„ ЩҮШ§ЫҢ ШұШіЩ… ШҙШҜЩҮШҢ ШҜЩҲ Щ…Ш«Щ„Ш« $ AEO$ ЩҲ $OCD$ ЩҮЩ…ЩҶЩҮШҙШӘ ЩҮШіШӘЩҶШҜ.
ЩҫШі:
$$ S_{ODB} + S_{OAB} = S_{DAB} $$
$$ \frac{1}{2}(EB+CB)Oh+\frac{1}{2}AB.OH= \frac{1}{2}(EB+CB).AK$$
ШЁШ§ ЩӮШұШ§Шұ ШҜШ§ШҜЩҶ $Oh= \frac{AK}{2} $ЩҲ ШЁШ§ ШіШ§ШҜЩҮ Ъ©ШұШҜЩҶ Ш№ШЁШ§ШұШӘ ШҜШ§ШұЫҢЩ…:
Щ…ЫҢ Ш®ЩҲШ§ЩҮЫҢЩ… Ш«Ш§ШЁШӘ Ъ©ЩҶЫҢЩ…:
$$ S_{EACB}=OH.AB $$
ШЁШ§ ШӘЩҲШ¬ЩҮ ШЁЩҮ ШҙЪ©Щ„ ЩҮШ§ЫҢ ШұШіЩ… ШҙШҜЩҮШҢ ШҜЩҲ Щ…Ш«Щ„Ш« $ AEO$ ЩҲ $OCD$ ЩҮЩ…ЩҶЩҮШҙШӘ ЩҮШіШӘЩҶШҜ.
ЩҫШі:
$$ S_{ODB} + S_{OAB} = S_{DAB} $$
$$ \frac{1}{2}(EB+CB)Oh+\frac{1}{2}AB.OH= \frac{1}{2}(EB+CB).AK$$
ШЁШ§ ЩӮШұШ§Шұ ШҜШ§ШҜЩҶ $Oh= \frac{AK}{2} $ЩҲ ШЁШ§ ШіШ§ШҜЩҮ Ъ©ШұШҜЩҶ Ш№ШЁШ§ШұШӘ ШҜШ§ШұЫҢЩ…:
$$ AB.OH= \frac{1}{2}(EB+CB).AK$$
Ъ©ЩҮ Ш№ШЁШ§ШұШӘ ШіЩ…ШӘ ШұШ§ШіШӘ ЩҮЩ…Ш§ЩҶ Щ…ШіШ§ШӯШӘ Ш°ЩҲШІЩҶЩӮЩҮ Ш§ШіШӘ ЩҫШі:
$$ S_{EACB}=OH.AB $$