طبق شکل زیر ارتفاع های ذوزنقه را رسم می کنیم:
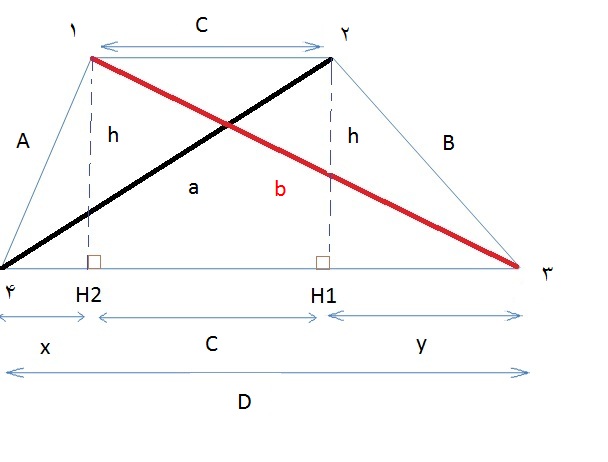می خواهیم ثابت کنیم:
$$ a^{2}+ b^{2}= A^{2}+ B^{2}+2CD $$
روابط زیر با استفاده از قضیه فیثاغورث به دست می آیند:
در مثلثهای $2 H_{1} 3 $ ، $1 H_{2} 3 $، $1 H_{2} 4 $ ،$2 H_{1} 4 $ داریم:
$$(C+x)+ h^{2}= a^{2}(1) $$
$$(C+y)+ h^{2}= b^{2}(2) $$
$$ x^{2}+ h^{2}= A^{2}(3) $$
$$ y^{2} + h^{2}= B^{2}(4) $$
$$x+C+y=D(5)$$
از رابطه های (1) و (3) و همچنین از رابطه های (2) و (4) با حذف $ h^{2} $ داریم:
$$ a^{2}- C^{2}-2Cx= A^{2} $$
$$ b^{2}- C^{2}-2Cy= B^{2} $$
با جمع کردن طرفین این رابطه ها داریم:
$$ a^{2}+b^{2} -2C(x+y+C)= A^{2}+B^{2} $$
با قرار دادن رابطه (5) در این رابطه حکم حاصل می شود:
$$ a^{2}+ b^{2}= A^{2}+ B^{2}+2CD $$
