نقطه $ \sqrt[3]{2} $ روی محور اعداد

Question

نقطه ی $ \sqrt[3]{2} $را بر محور مشخص کنید.

Comments

rezasalmanian@

پس با این اوصاف و باتوجه به دیدگاه  admin, فقط اونایی رو میشه رسم کرد که فرجه رادیکال توانی از 2 باشه.

---

فرجه های بالاتر قابل رسم است.

---

@fardina

میتونم بپرسم ایراد پاسخی که گذاشته بودین چی بود؟؟؟و اینکه لطف کنید به دیدگاهی که من برای پاسختون نوشته بودم جواب بدین

---

حقیقتش دارم روش فکر میکنم.

ولی برای $\sqrt[4]2$ میتونید به اینجا نگاه بندازید: http://math.irancircle.com/440
و به طریق مشابه میتونید تمام رادیکال های با فرجه توانی از 2 رو رسم کنید. مثلا چون $\sqrt[4]2$ قابل رسمه یک رو هم کنارش بکشیم آنگاه $x^2=\sqrt[4]2\times 1$ و لذا $x=\sqrt[8]2$ .

---

@fardina

بله مراجعه کردم و کاملا واضح و قابل درک هستش ولی من با نکته ای که در مورد غیر مدرج بودن خط کش فرمودین مشکل دارم.بسیار خب,هر موقع که به نتیجه رسیدین,مثل همیشه از اطلاعاتتون استفاده می کنیم.سپاسگزار

Answer 1

می تونید در اینجا اثبات اینکه $\sqrt[3 ]2$ با خط کش و پرگار قابل رسم نیست رو ببینید: Doubling the cube

این مساله به مساله تضعیف مکعب مشهور بوده و در سال 1837 Pierre Wantzel ثابت کرده است که تضعیف مکعب با خط کش و پرگار قابل رسم نیست. در واقع اثبات با تبدیل مساله به یک مساله جبری انجام می شود. ثابت می شود که یک عدد $\alpha$ ساختنی است هرگاه در یک چندجمله ای تحویل ناپذیر روی $\mathbb Q[x]$ با درجه ی توانی از $2$ صدق کند. لذا برای $\alpha=\sqrt[3 ]2$ داریم $\alpha^3=2$ پس $x^3-2\in\mathbb Q[x]$ و بنابر قضیه ذکر شده $\sqrt[ 3]2$ قابل رسم نیست.

توجه کنید که خط کش و پرگاری که ما استفاده کنیم به ترتیب زیر هستند:

پرگار می تواند در هر اندازه دلخواهی باز شود ولی هیچ نشانه گذاری ای روی آن وجود ندارد. دایره ها را در صورتی می توانید بکشید که دو نقطه داشته باشید، یکی به عنوان مرکز و دیگری نقطه ای روی دایره.

خط کش به اندازه نامتناهی بلند بوده و هیچ نشانه گذاری ای روی آن وجود ندارد. و برخلاف خط کش های معمولی فقط یک لبه دارد. از آن فقط برای ترسیم یک خط بین دو نقطه ی داده شده و یا امتداد یک خط داده شده می توان استفاده کرد.

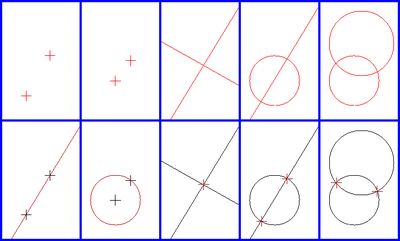
در واقع ترسیمات پایه ای با این خط کش و پرگار عبارت اند از(شکل زیر را ببینید):

• رسم خط بین دو نقطه ی داده شده
• رسم دایره گذرا از یک نقطه و به مرکز یک نقطه ی دیگر
• ایجاد کردن یک نقطه از اشتراک دو خط ناموازی داده شده
• ایجاد کردن یک یا دونقطه از برخورد خط و دایره(اگر با هم اشتراک داشته باشند)
• ایجاد کردن یک یا دو نقطه از برخورد دو دایره با هم( اگر با هم اشتراک داشته باشند)

---

حالت قابل رسم:

و برای حالتی که قابل رسم هست در همان صفحه با استفاده از ترسیم neusis و استفاده از یک خط کشی که تعریف خاص خود را دارد و با خط کش معمولی فرق دارد اثبات شده است. امیدوارم که این حالت گمراه کننده نباشد و به شما القا نکند که $\sqrt[3 ]2$ قابل رسم است! چون خط کشی که او استفاده میکند تعریف کاملا متفاوتی با خط کش معمولی مورد استفاده ما دارد. با خط کشی که او تعریف می کند حتی تثلیث زاویه هم امکان پذیر است. ممکن است شما هم یک خط کش با تعریف خاص خودتان از آن بتوانید ریشه سوم عدد دو را رسم کنید!

ترسیم neusis:

خط کش neusis دارای این خاصیت است که برای دو خط داده شده ی $l,m$ و یک پاره خط با طول داده شده ی $a$ می توان خطی رسم کرد که از این دو خط عبور کرده و از نقطه ی داده شده ی $P$ (که به قطبی neusis معروف است) عبور کند به طوریکه فاصله ی دو نقطه ی ایجاد شده از برخورد این خط با خطوط $l,m$ دارای طول $a$ باشد. در اینصورت با استفاده از این خط کش به ترتیب زیر می توان $\sqrt[3 ]2$ را رسم کرد:

• یک خط کش را با طول داده شده ی $a=1$ در نظر بگیرید.
• مثلث متساوی الاضلاع $ABC$ را رسم کنید.
• ضلع $AB$ را به همان مقدار امتداد دهید تا به $D$ برسید.
• از $BC$ نیم خط $CE$ رارسم کنید
• با امتداد $DC$ نیم خط $CF$ را رسم کنید.
• حال با استفاده از خاصیت خط کش neusis پاره خط $AH$را طوری رسم میکنیم که از نقطه ی $A$ عبور کند و فاصله ی $GH$ برابر $a=1$ باشد.

در اینصورت می توان ثابت کرد $AG=\sqrt[3 ]2$.

در هر صورت توجه بفرمایید که این حالت قابل رسم با استفاده از اضافه کردن خاصیتی است که خط کش معمولی تعریف شده در بالا دارای آن خاصیت نیست.

Comments

یه مقدار مطالب بالا واسم گنگه!
طریقه ی اثبات اینکه $AG$ برابر با ریشه سوم 2 ,به چه شکل هستش؟

---

نکته ی مهم در حرفای من این هستش که $\sqrt[3]2$ قابل رسم نیست!
من فقط با توجه به صفحاتی که ارجاع دادم در مورد غیرقابل ترسیم بودن $\sqrt[3]2$ مطالبی رو جمع کردم. اثبات غیر قابل رسم بودن در تمام کتاب های جبری موجوده. معمولا در جبر 2 خونده میشه.
در مورد حالت قابل رسم با خط کش neusis نمیدونم چرا میشه $\sqrt[3]2$! من یک سوال مشابه میپرسم.

---

سلام آیا می توانیم پرگار را به اندازه ای مثلا بین دو نقطه به دست آمده باز کنیم واین شعاع را در جای دیگر استفاده کنیم.

---

@امیر
سلام. سوال خوبی پرسیدید. پرگار اصضلاحا بهش میگیم پرگار فروریختنی یعنی با جابجا کردن پرگار ، به هم میریزه. https://en.wikipedia.org/wiki/Compass-and-straightedge_construction
در همین صفحه توضیح داده که این محدودیت مهم نیست چون در اینجا https://en.wikipedia.org/wiki/Compass_equivalence_theorem قضیه ای اومده که گفته هر ترسیمی که با پرگار ثابت انجام بشه میتونه با پرگار فروریختنی هم به دست بیاد.
یعنی چنانچه سه نقطه A,B,C رو به ما داده باشن میتونیم دایره ای به مرکز A و شعاع BC رسم کرد.