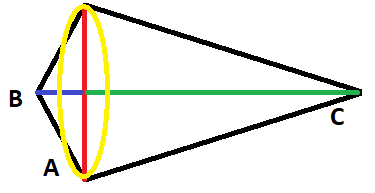
نخست توجه کنید که وتر سهگوشتان برابر است با $\sqrt{5^2+(12)^2}$ که ۱۳ میشود. اکنون اندازهٔ ارتفاع وارد بر این یال را با $h$ نمایش دهید و میتوانید با توجه به اینکه مساحت یک سهگوش یک عدد ثابت است و اینکه از چه ارتفاع و قاعدهای استفاده کنید فرقی نمیسازد بدست بیاورید. ارتفاع سهگوشتان برابر است با
$$\frac{1}{2}AB\times AC=\frac{1}{2}BC\times h$$
که با جایگذاری اندازهٔ سه یال خواهید داشت $h=\frac{61}{13}$. اکنون تنها دو اندازهٔ دیگر مانده است تا بتوانید حجم دو مخروطی که میخواهید را بیابید. باید اندازهٔ دو پارهخط مشخص شده با رنگهای آبی و سبز که در واقع از محل برخورد ارتفاعی که طولش را محاسبه کردید تا دو گوشتهٔ $B$ و $C$ هستند. توجه کنید که دو سهگوش قائمالزاویه دارید که یک ضلعشان مشترک و اندازهاش همان $h$ است و وترهایشان $AB$ و $AC$ هستند که اندازهشان را دارید، خیلی راحت اندازهٔ یال آخرشان را میتوانید بیابید. اندازهٔ پارهخط آبی را با $\ell$ نشان دهید آنگاه برای سبز رنگ اندازهاش میشود $13-\ell$. برای آبیرنگ از رابطهٔ بابلیان (که به اسم فیثاغورس زدهاند) استفاده میکنیم.
$$\ell=\sqrt{5^2-(\frac{60}{13})^2}=\frac{25}{13}$$
اکنون حجم شکل که جمع حجم دو مخروط است؛
$$\frac{1}{3}\pi(\frac{60}{13})^2\frac{25}{13}+\frac{1}{3}\pi(\frac{60}{13})^2(13-\frac{25}{13})=\frac{1200}{13}\pi\simeq 289.99$$
البته اگر توجه کنید نیاز به بدستآوردن درازای پارهخاطهای آبی و سبز نداشتید زیرا با سادهکردن جمع فرمول دو مخروط دارید؛
$$\frac{1}{3}\pi h^2\ell+\frac{1}{3}\pi h^2(|BC|-\ell)=\frac{1}{3}\pi h^2(\ell+|BC|-\ell)=\frac{1}{3}\pi h^2|BC|$$
که منظور از $|BC|$ درازای یالِ $BC$ است. پس فقط کافی بود اندازهٔ یال $BC$ و ارتفاع وارد بر آن را بدانید.