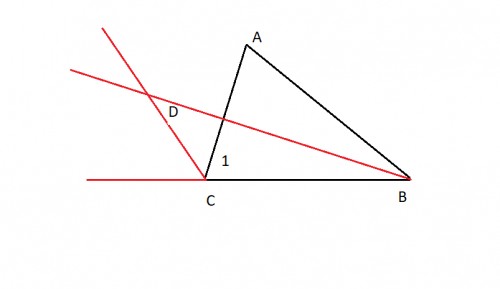
Щ…Ш№Ш§ШҜЩ„ЩҮ ШІШ§ЩҲЫҢЩҮ D ШұШ§ Щ…ЫҢЩҶЩҲЫҢШіЫҢЩ…:
$ D=180-( \dfrac{A+B}{2}+ C_{1}+ \dfrac{B}{2} )$
ШЁШұШ§ЫҢ ШІШ§ЩҲЫҢЩҮ A ЩҮЩ… Щ…ЫҢЩҶЩҲЫҢШіЫҢЩ…:
$A=180-(B+ C_{1} )$
Щ…ЫҢШӘЩҲЩҶЫҢЩ… ШіШ§ШҜЩҮ Ъ©ЩҶЫҢЩ… ЩҲ ШЁЩҶЩҲЫҢШіЫҢЩ…:
$\dfrac{A}{2}+ C_{1}+B+D=180$
$B+ C_{1} +A=180$
ЪҶЩҲЩҶ ЫҢЪ© Ш·ШұЩҒ ШҜЩҲ Щ…Ш№Ш§ШҜЩ„ЩҮ ШЁШұШ§ШЁШұ Ш§ШіШӘ ШҜЩҲ Ш·ШұЩҒ ШҜЫҢЪҜШұ ШұШ§ Щ…ШіШ§ЩҲЫҢ ЩҮЩ… ЩӮШұШ§Шұ Щ…ЫҢШҜЩҮЫҢЩ… ЩҲ ЩҫШі Ш§ШІ ШіШ§ШҜЩҮ ШіШ§ШІЫҢ ЩӮШ¶ЫҢЩҮ Ш§Ш«ШЁШ§ШӘ Щ…ЫҢШҙЩҲШҜ.Ш§ЪҜШұ ШіЩҲШ§Щ„ЫҢ ШҜШ§ШұЫҢ ШЁЩҫШұШі.