به محفل ریاضی ایرانیان خوش آمدید! لطفا برای استفاده از تمامی امکانات عضو شوید
پرسش سوال

هندسه_ اثبات زاویه ی بین ارفاع وارد بر وتر نیمساز برابر با نصف قدر مطلق تفاضل دوزاویه تند

0 امتیاز
2,858 بازدید
در دبیرستان توسط نگین (1 امتیاز)

ثابت کنید زاویه بین ارتفاع وارد بر وتر و نیمساز زاویه قائم، برابر است با نصف(قدر مطلق) تفاضل دو زاویه تند (حاده) مثلث.

1 پاسخ

0 امتیاز
توسط mdardah (1,636 امتیاز)
ویرایش شده توسط mdardah

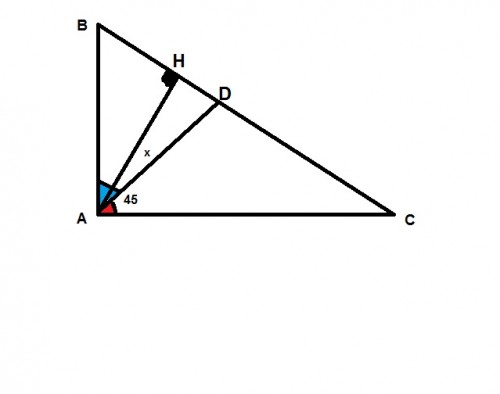
درمثلث ABC اگر زاویه Aمساوی90 درجه باشد وزاویه بین ارتفاع ونیمساز را xدرنظر بگیریم داریم $ \angle x+45+ \angle c=90 $ و در مثلث قائم الزاویهABH داریم$ \angle B+45- \angle x=90$اگردو طرف رابطه را مساوی قراردهیم داریم 2x=$ \angle B- \angle C $ در نتیجه چون تفاضل دوزاویه ممکن است منفی باشد مقدار

$x= \frac{1}{2} | B- \angle C | $

چگونه می توانم به محفل ریاضی کمک کنم؟

کانال تلگرام محفل ریاضی

سوالات مشابه

“ ریاضیدان، کسی است که شباهت ها را بین قضایا دریابد. ریاضیدان بهتر کسی است که بتواند شباهت بین برهان ها را ببیند. بهترین ریاضیدان کسی است که بتواند به شباهت بین نظریه ها توجه کند. و می توان تصور کرد که ریاضیدان نهایی کسی است که بتواند شباهت بین شباهت ها را مشاهده کند.
...