بنام خدا.از p وسط BCخطی موازی AB رسم می کنیم تا AC رادر M قطع کندطبق قضیه تالس داریم $ \frac{CP}{PB} = \frac{CM}{MA}= 1$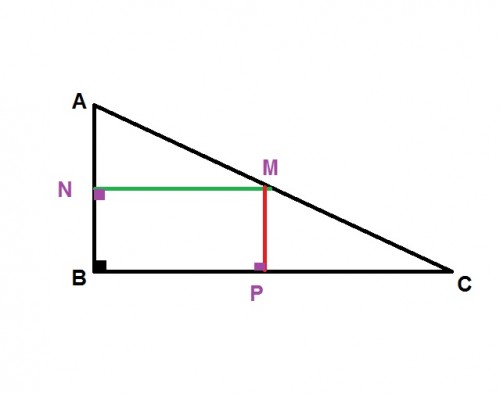
یعنیM وسط AC است.حال ازنقطه M خطی موازی BC رسم میکنیم تا AB رادر نقطه N قطع کندچون MN موازی BC است بنابراین زاویه N قائمه است بار دیگر قضیه تالس را می نویسیم $ \frac{AM}{MC} = \frac{AN}{NP} =1 $ عدد1 به این دلیل است که صورت ومخرج کسر اول مساویند.بنابراین AN=NB یعنی نقطه N وسط AB است وچون زاویه N قائمه است یعنی MN عمود منصف AB میباشد از نقطه P نیز موازی AB رسم کرده بودیم MP هم عمود منصف BC است این دو عمود منصف همدیگر رادر نقطه M وسط AC قطع کرده اند حال اگر از نقطه M خطی عمود اخراج کنیم چون Mوسط AC است عمود منصف AC نیز از M میگذرد یعنی سه عمود منصف در نقطه M همرسند.