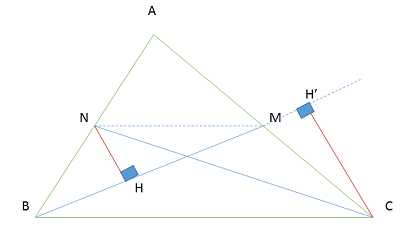
بنابر شکل $NH$ ارتفاع مثلث های $BON$و $MON$ است لذا $\frac{S_{BON}}{S_{OMN}}=\frac{BO}{OM}$
از طرفی $CH'$ ارفاع مثلث های $BOC$و $COM$ است لذا $\frac{S_{BOC}}{S_{COM}}=\frac{BO}{OM}$
بنابراین از دو تساوی بالا داریم
$$\frac{S_{BON}}{S_{OMN}}=\frac{S_{BOC}}{S_{COM}}\tag{*}\label{*}$$
بنابر فرضیات مساله $\frac{8}{S_{OMN}}=\frac{S_{BOC}}{3}$ یعنی $S_{OMN}\times S_{BOC}=24$
اما ارتفاع های مثلث های $ANM$و $BNM$ برابر هستند( ارتفاعی که از راس $M$ بر $AN$ وارد می شود.) بنابراین $\frac{S_{ANM}}{S_{BNM}}=\frac{AN}{BN}$
و همینطور ارتفاع مثلث های $ANC$ و $BNC$ یکی است(ارتفاعی که از $C$ بر $AB$ وارد می شود) بنابراین $\frac{S_{ANC}}{S_{BNC}}=\frac{AN}{BN}$ و این یعنی $$\frac{S_{ANM}}{S_{BNM}}=\frac{S_{ANC}}{S_{BNC}}\tag{**}$$
و یا بطور معادل $\frac{5}{8+S_{OMN}}=\frac{3+S_{OMN}+5}{8+S_{OBC}}$
با استفاده از $\eqref{*}$ و چاگذاری در تساوی بالا و طرفین وسطین و حل معادله باید به جواب برسید.