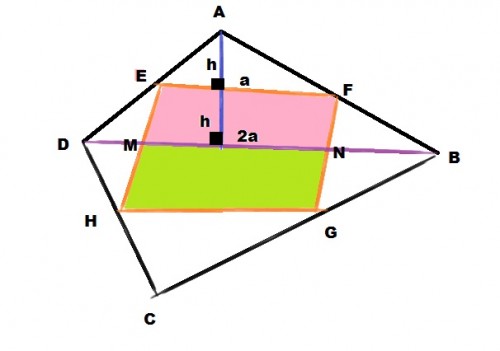
بنام خدا.طبق شکل زیر وقضیه تالس داریم چون E وF اوساط دوضلع AD و AB هستند
$ \frac{AE}{AD} = \frac{EF}{DB} = \frac{1}{2} $ یعنی EF نصف BD می باشد چهارضلعی EFGH طبق قضیه عکس تالس متوازی الاضلاع است بنا براین چهار ضلعی EFNM نیز متوازی الاضلاع است و مساحت آن برابر ah می باشد و مساحت مثلث ABD برابر$ \frac{2a.2h}{2} =2ah $ یعنی مساحت EFNM نصف مثلث ABD میباشد به همین ترتیب مساحت MNGH نصف مثلث DBC مباشد در نتیجه مساحت EFGH نصف چهارضلعی ABCD میباشد.