آیا واقعا $ \sqrt[3]{-1}= \frac{1+ i\sqrt{3} }{2} $ است؟

Question

سلام خدمت تمام دوستان و اساتید سایت محفل ریاضی

پرسشی مدت ها ذهنم را درگیر کرده است:

$ \sqrt[3]{-1} $ مقدار عددی این عبارت را با استفاده از دستور N در نرم افزار Mathematica محاسبه می‌کنیم...به ما عدد مختلط$0.5+0.866025i$ را می‌دهد.

حالا مقدار عددی $ \frac{1+ i\sqrt{3} }{2} $ را در نرم افزار Mathematica محاسبه می‌کنیم...این‌بار هم به ما عدد مختلط $0.5+0.866025i$ را می‌دهد!

پس آیا می‌توان گفت که این دو عبارت با هم برابر هستند؟! یا اگر واقعا با هم برابر هستند،دلیل آن چیست.

با تشکر.

Comments

@Amirmza بله برابر هستند ولی این فقط یکی از ریشه های سوم $-1$ است، $-1$ دقیقاً سه ریشه سوم دارد.

Answer 1

وابسته به اینکه چگونه از نرم‌افزار Mathematica بخواهید که $\sqrt[3]{-1}$ را محاسبه کند، ممکن است خروجی‌های متفاوتی بگیرید. یک روش استفاده از دستورِ Surd است. این دستور دو ورودی می‌گیرد $n$ و $x$ که یکُمی برای فرجه و دومی برای عدد زیر رادیکال است. فرجه را فقط عدد صحیح می‌پذیرد. در صورت انتخاب فرجهٔ زوج، برای $x$های منفی خروجی‌تان Indeterminate می‌گیرد و یک error که می‌گوید دستور Surd با فرجهٔ زوج بر روی اعداد منفی اثر نمی‌کند. به هر حال با اجرای دستور زیر برای $\sqrt[3]{-1}$ خروجی‌ِ $-1$ را خواهید گرفت.

Surd[-1,3]

راه دیگر استفاده از دستور CubeRoot است که ریشهٔ حقیقی سوم عدد حقیقی را می‌گیرد.

CubeRoot[-1]

راه دیگر استفاده از توان کسری است.

(-1)^(1/3)

که خروجی‌تان به شکل $(-1)^{1/3}$ نمایش داده می‌شود. اکنون اگر آن را بخواهید با دستور N به شکل عددی اعشاری ببینید به 0.5+0.866025i می‌رسید که در واقع با مقدار عددی کسری که اشاره کردید برابر است. توان را به جای استفاده از نماد ^ می‌توان با نوشتن دستور Power نیز انجام داد.

Power[-1,1/3]

اما برویم به سراغ روشی دیگر، یعنی استفاده از حل برابری. اگر حل دقیق بخواهیم از دستور Solve و اگر حل عددی بخواهیم از دستور NSolve استفاده می‌کنیم. باید توجه کنید که NSolve الزاما فقط اثر دادن N بر روی خروجیِ Solve نیست و گاها N[Solve[]] می‌تواند حاصلی متفاوت از NSolve بدهد. ولی در خیلی از مواقع یکی خواهند شد. $\sqrt[3]{-1}$ را می‌توان اینگونه گفت که چه عدد یا عددهایی به توان ۳ برسند و برابر با $-1$ شوند. یا به عبارت دیگر ریشه‌های $x^3=-1$ یا همان $x^3+1=0$.

Solve[x^3==-1,x]

یا

Solve[x^3+1==0,x]

در هر دو صورت به خروجیِ زیر می‌رسید.

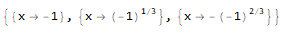
اکنون توجه کنید که ۳ ریشهٔ مختلط برابری (معادله)مان را داده‌است. بنا به قضیهٔ اساسی جبر می‌دانید که هر معادلهٔ چندجمله‌ایِ تک‌متغیره با ضرایب مختلط (و به طبع حقیقی و یا گویا) به تعداد درجه‌اش ریشهٔ مختلط دارد (با احتساب تکرارشان). اینجا هم معادلهٔ درجهٔ ۳ دارید پس انتظار دیدن ۳ ریشهٔ مختلط دارید. اما نمایش این سه ریشه به این شکل نمادین شاید برایتان جالب نباشد پس از آن N می‌گیرید یا اینکه از اول NSolve می‌زنید. و پاسخ زیر را می‌گیرید.

اکنون برویم به سراغ ابهام شما. اینکه می‌گوئید خروجیِ متمتیکاییِ $(1-)^{\frac{1}{3}}$ با عدد $\frac{1+i\sqrt{3}}{2}$ برابر است، حرف درستی است. و این تناقضی با اینکه دو عدد دیگر نیز ریشهٔ سوم عدد منفی یک هستند یعنی عددهای $-1$ و $\frac{1-i\sqrt{3}}{2}$ ندارد. چرا؟ چون همانطور که توسعه‌دهندگانِ نرم‌افزار Mathematica در راهنمای نرم‌افزارشان برای دستور Surd نوشته‌اند که تنها یک پاسخ حقیقی از ریشه‌ها را به شما خواهد داد، برای دستور Power در راهنمای نرم‌افزارشان نیز نوشته‌اند که این دستور برای توان کسری همهٔ ریشه‌ها را نخواهد داد و تنها یک ریشهٔ مختلط اصلی را می‌دهد. در راهنمای Mathematica برای دستور Power به بخشِ Possible Isssues (یعنی مشکل‌های ممکن) نگاه کنید.

Power always computes principal roots

و دقیقا مثال شما را زده‌اند یعنی

برای تعریف ریشهٔ اصلی می‌توانید به این صفحهٔ واژه‌نامهٔ ویکی‌پدیا نگاه کنید: (روی اینجا کلیک کنید). برای یک عدد طبیعیِ $n$ و یک عدد مختلط دلخواهِ $a$ ریشهٔ اصلیِ $n$اُمِ $a$ یعنی عدد مختلطی که به توان $n$ برسد برابر با $a$ بشود و بزرگترین قسمت حقیقی را نسبت به تمام عددهای مختلط دیگری که چنین ویژگی‌ای دارند دارا باشد، و اگر چند عدد مختلط با قسمت حقیقی یکسان و بزرگتر از مابقی وجود داشتند، آنگاه آن عددی که قسمت موهومی‌اش مثبت است (برای نمون ریشه‌های دوم منفی یک از قسمت آخر برای تعیین ریشهٔ اصلی‌اش استفاده می‌کند). پس الآن مشخص است که چرا از بین ۳ عددی که هر سه ریشهٔ سوم منفی یک هستند، عددی که شما اشاره کردید را ارائه می‌کند.

در آخر شاید بد نباشد به قسمت‌های دیگر بخش Possible Issues نیز توجه کنید تا در مثال‌های دیگر دچار مشکل نشوید. برای نمونه توسعه‌دهندگان تأکید کرده‌اند که انتظار نداشته‌باشید که اگر از Mathematica خواستید عبارت $(z^3)^{\frac{1}{3}}$ را حساب کند، به شما $z$ را بدهد :)

Comments

@AmirHosein بسیار سپاسگزارم از توضیحات شما.

---

@AmirHosein بنابراین هر عدد منفی سه ریشه سوم دارد؟

---

@Amirmza بلی هر عدد مختلطی و به طبع هر عدد حقیقی چه مثبت چه منفی دارای $n$ ریشهٔ $n$اُمِ مختلط است. که البته برای عدد صفر تمام $n$ ریشه‌اش تکراری و برابر صفر است.

---

@AmirHosein سپاس.

Answer 2

به کمک اتحادمکعب دوجمله ای چون داریم:

$ (\frac{1+i \sqrt{3}}{2})^{3}= \frac{1+3\sqrt{3}i-9-3\sqrt{3}i}{8}=-1 $

پس

$ \frac{1+i \sqrt{3}}{2}= \sqrt[3]{-1} $

Answer 3

$-1=e^{\pi i }\Longrightarrow e^{\frac{\pi i}{3}}=\cos({\frac{\pi }{3}})+i\sin ({\frac{\pi }{3}})=\frac{1}{2}+i\frac{\sqrt{3}}{2} $

Comments

@mdgi پس چرا با وارد کردن معادله در نرم افزار Mathematica این جواب را هم به ما می‌دهد؟

---

درست فرمودید. معادله  $x^2+x+1=0$ دارای ریشه های $\frac{-1\pm i\sqrt{3}}{2}$ است

---

@mdgi اگر $ \sqrt[3]{-1}=-1 $ می‌باشد،پس چرا نرم افزار Mathematica مقدار عددی این عبارت را عددی مختلط به ما می‌دهد؟

---

درواقع $\sqrt[3]{z}$ همواره سه تا جواب دارد.  و $\sqrt[3]{-۱}=\lbrace -1, \frac{-1\pm i\sqrt{3}}{2}\rbrace$

---

@mdgi ممنون از شما.با تشکر فراوان.