Ш§ШӯШӘЩ…Ш§Щ„Ш§ Щ…ШӘЩҶ ЩҫШұШіШҙвҖҢШӘШ§ЩҶ ШұШ§ Ш§ШҙШӘШЁШ§ЩҮ ЩҶЩҲШҙШӘЩҮвҖҢШ§ЫҢШҜ. Ш§ЪҜШұ ЩҒШұШ¶ Ъ©ЩҶЫҢЩ… Ъ©ЩҮ Щ…ЩҶШёШұЩҲ Щ…ШӘЩҶвҖҢШӘШ§ЩҶ Ш§ШіШӘ Ъ©ЩҮ В«ЫҢЪ© ЪҜШұШ§ЩҒ ЩҶШ§ЩҮЩ…ЫҢЩ„ШӘЩҲЩҶЫҢ Ш§ШіШӘ Ш§ЪҜШұ ЩҲ ШӘЩҶЩҮШ§ Ш§ЪҜШұ ЪҜШұШ§ЩҒЫҢ ШҜЩҲШЁШ®ШҙЫҢ ШЁШ§ ШӘШ№ШҜШ§ШҜ ЩҶШ§ШЁШұШ§ШЁШұЫҢ ЪҜШұЩҮ ШҜШұ ШҜЩҲ ШЁШ®ШҙШҙ ШЁШ§ШҙШҜВ» Ъ©ЩҮ Ш§ШөЩ„Ш§ ЩҮЩ…ЫҢЩ„ШӘЩҲЩҶЫҢ ШЁЩҲШҜЩҶ ЩҲ ЩҶШЁЩҲШҜЩҶ Ш§Щ„ШІШ§Щ…ЫҢ ШЁЩҮ ШҜЩҲШЁШ®ШҙЫҢ ШЁЩҲШҜЩҶ ЩҶШҜШ§ШұШҜ.
- ШҜЩҲШЁШ®ШҙЫҢ Ъ©ЩҮ ЩҮЩ…ЫҢЩ„ШӘЩҲЩҶЫҢ ШЁШ§ШҙШҜ:
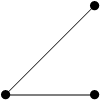
- ШҜЩҲШЁШ®ШҙЫҢ Ъ©ЩҮ ЩҮЩ…ЫҢЩ„ШӘЩҲЩҶЫҢ ЩҶШЁШ§ШҙШҜ:
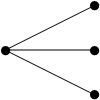
- ЩҶШ§ШҜЩҲШЁШ®ШҙЫҢ Ъ©ЩҮ ЩҮЩ…ЫҢЩ„ШӘЩҲЩҶЫҢ ШЁШ§ШҙШҜ:
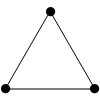
- ЩҶШ§ШҜЩҲШЁШ®ШҙЫҢ Ъ©ЩҮ ЩҮЩ…ЫҢЩ„ШӘЩҲЩҶЫҢ ЩҶШЁШ§ШҙШҜ:
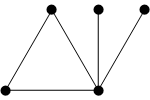
ЩҫШі Ш§ШөЩ„Ш§ ЪҜШІШ§ШұЩҮвҖҢШ§ЫҢ Ш§ЪҜШұ ЩҲ ШӘЩҶЩҮШ§ Ш§ЪҜШұ ШЁШұШ§ЫҢ ЩҮЩ…ЫҢЩ„ШӘЩҲЩҶЫҢ (ЫҢШ§ ЩҶШ§ЩҮЩ…ЫҢЩ„ШӘЩҲЩҶЫҢ) ШЁШ§ ШҙШұШ· ШҜЩҲШЁШ®ШҙЫҢ ЩҶЩ…ЫҢвҖҢШӘЩҲШ§ЩҶЫҢШҜ ШЁШіШ§ШІЫҢШҜ (ЪҶЩҮ ШӘШ№ШҜШ§ШҜ ЪҜШұЩҮвҖҢЩҮШ§ ШҜШұ ШҜЩҲ ШЁШ®Шҙ ЫҢЪ©ЫҢ ШЁШ§ШҙШҜ ЪҶЩҮ ЩҶШЁШ§ШҙШҜ).
Ш§Ъ©ЩҶЩҲЩҶ Ш§ЪҜШұ Щ…ЩҶШёЩҲШұШӘШ§ЩҶ ЩҒЩӮШ· ЪҜШІШ§ШұЩҮЩ” ЫҢЪ©вҖҢШ·ШұЩҒЩҮ ЩҲ ШўЩҶ ЩҮЩ… ШҜШұ ШіЩ…ШӘ ШЁШұШ№Ъ©Ші ЪҶЫҢШІЫҢ Ъ©ЩҮ ЩҶЩҲШҙШӘЫҢШҜ ШЁШ§ШҙШҜШҢ ЫҢШ№ЩҶЫҢ В«ЫҢЪ© ЪҜШұШ§ЩҒ ШҜЩҲШЁШ®ШҙЫҢ ШЁШ§ ШӘШ№ШҜШ§ШҜ ЩҶШ§ШЁШұШ§ШЁШұ ЪҜШұЩҮ ШҜШұ ШҜЩҲ ШЁШ®ШҙШҙ ШӯШӘЩ…Ш§ ЩҶШ§ЩҮЩ…ЫҢЩ„ШӘЩҲЩҶЫҢ Ш§ШіШӘВ» Ъ©ЩҮ ШҜШұ Ш§ЫҢЩҶ ШөЩҲШұШӘ ЩҶЩ…ЩҲЩҶЩҮЩ” ШҙЩ…Ш§ШұЩҮЩ” Ыұ ШҜШұ ШЁШ§Щ„Ш§ ШЁШұШ§ЫҢШӘШ§ЩҶ Щ…Ш«Ш§Щ„ ЩҶЩӮШ¶ Ш§ШіШӘ. ШЁШұШ§ЫҢШӘШ§ЩҶ ЩҮЩ… ШЁШ§ЫҢШҜ (Ш§ШІ ЩӮШіЩ…ШӘ ЩҶШ®ШіШӘ ЩҫШ§ШіШ®) ШұЩҲШҙЩҶ ШЁШ§ШҙШҜ Ъ©ЩҮ ЪҶШұШ§ Ш§ШөЩ„Ш§ ШЁЩҮ ШіШұШ§Шә ШіЩ…ШӘ ШҜЫҢЪҜШұ ЪҜШІШ§ШұЩҮ ШЁЩҮ ШҙЪ©Щ„ ЫҢЪ© Ш·ШұЩҒЩҮ ЩҶШұЩҒШӘЩ….