دو مثلث $OBN$ و $OAM$ بنا به حالت سه ضلع مساوی هستند. پس زوایای $OND$ و $OMD$ مساویند. دو ضلع $DM$ و $DN$ را امتداد میدهیم و از $O$ بر آنها عمود میکنیم:
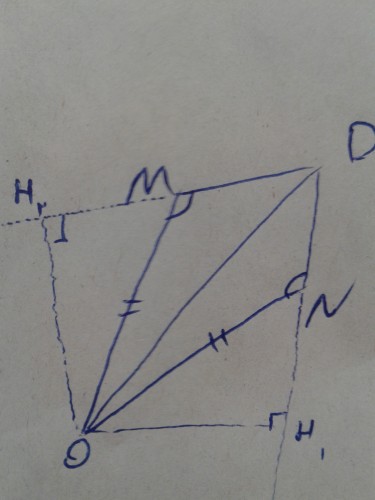دو مثلث
$OH_1N$ و
$OH_2M$
بنا به حالت وتر و یک زاویه با هم برابرند و نتیجه میشود دو مثلث
$OH_1D$ و $OH_2D$
با هم برابرند. بنابراین نتیجه میگیریم که دو مثلث
$OMD$
و
$OND$
بنا به حالت زض ز مساویند و درنهایت چون $ND=MD$ نتیجه میشود دو مثلث $BOD$ و $AOD$ بنا به حالت سه ضلع مساویند.
