بنده قضیه را بصورت زیر ثابت کردم:
بدون اینکه به کلیت مساله خللی وارد شود ابتدا مینویسیم $2R^2=R^2+R^2$ و هر $R$ را هم یکی از اضلاع مثلث قائم الزاویه متساوی الساقین مطابق شکل زیر در نظر می گیریم:
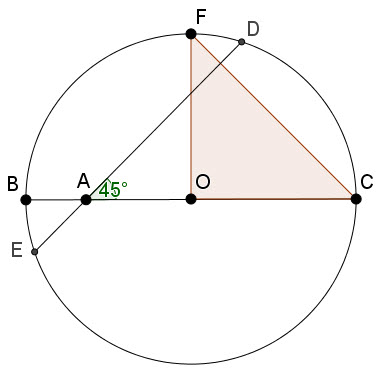
پس $2R^2=R^2+R^2=OC^2+OF^2=FC^2$ حالا حکم مساله بصورت $AD^2+AE^2=FC^2$ خواهد شد.
چون که $BC$ قطر دایره است ابتدا پاره خط $AE$ را نسبت به قطر $BC$ بازتاب میدهیم و آنرا $AM$ مینامیم(شکل زیر):
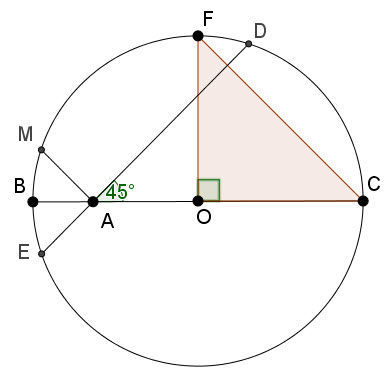
چون که زاویه $DAC=BAE=BAM=45^o$ پس $DAM=90^o$ و مثلث $DAM$ در راس $A$ قائم الزاویه خواهد شد(شکل زیر):
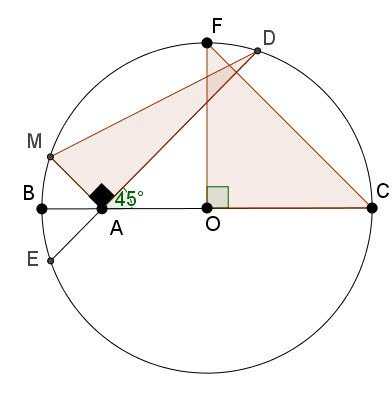
در این صورت $DA^2+AE^2=DA^2+AM^2=DM^2$ و حکم مساله بصورت زیر خواهد شد:
$DM^2=FC^2$
حال مثلث متساوی الساقین $DOM$ را تشکیل داده و ثابت می کنیم $DOM=90^o$(شکل زیر):
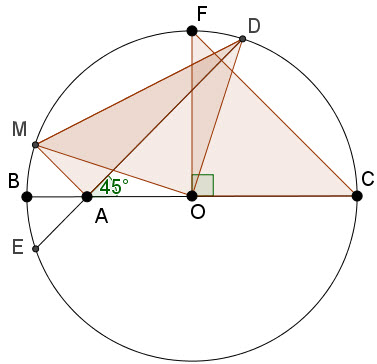
می دانیم اگر دو وتر دایره به نام های $DE$ و $BC$ همدیگر را در نقطه ای مانند $A$ قطع کنند آنگاه زاویه بین دو وتر یعنی $DAC$ از رابطه زیر بدست می آید:
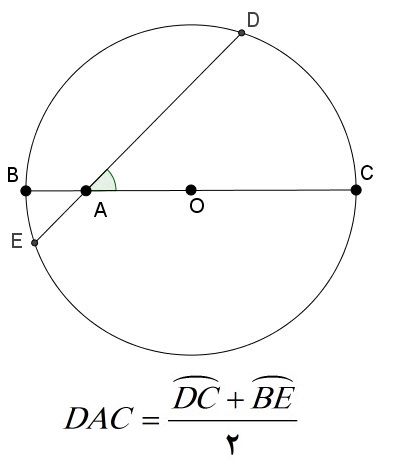
و چون $DAC=45^o$ پس $DC+BE=90^o$ و چون که $BE=BM$ پس $DC+BM=90^o$ در نتیجه کمان $MD$ برابر خواهد شد با :
$MD=180-(DC+BM)=180-90=90$
پس مثلث $DAM$ هم قائم الزاویه متساوی الساقین و با مثلث $FOC$ هم نهشت خواهد و $MD=FC$.
پس در نتیجه $FC^2=2R^2=MD^2=AD^2+AM^2=AD^2+AE^2$ و حکم مساله ثابت میشود.