ШЁШұШ§ЫҢ ШӯЩ„ Ш§ЫҢЩҶ ШіЩҲШ§Щ„ ШӘШ№ШұЫҢЩҒ Щ…ЫҢЪ©ЩҶЫҢЩ… $t:=\cos(\alpha)$ ЩҲ ЩҮЩ…ЪҶЩҶЫҢЩҶ ШЁШ§ Ш§ШіШӘЩӮШұШ§ Ш§Ш«ШЁШ§ШӘ Щ…ЫҢШҙЩҲШҜ Ъ©ЩҮ
$x_{n+1}=2x_n^2-1 \ \Rightarrow \ x_n=\cos(2^{n}\alpha)$
ШЁШ§ ШӘЩҲШ¬ЩҮ ШЁЩҮ Ш®ЩҲШ§ШіШӘЩҮ ШіЩҲШ§Щ„ ШЁШ§ЫҢШҜ ШҜШ§ШҙШӘЩҮ ШЁШ§ШҙЫҢЩ….
$ x_{11}=1 \ \Rightarrow \ \cos(2^{11}\alpha)=1 \ \Rightarrow \ 2^{11}\alpha=2k\pi \ \Rightarrow \ \alpha=\dfrac{2k\pi}{2^{11}} \ \Rightarrow \ t = \cos \alpha = \cos\left(\dfrac{k\pi}{2^{10}}\right) $
ЪҜЩҒШӘЩҮ ШҙШҜЩҮ ЪҶЩҶШҜ $t $ ЩҲШ¬ЩҲШҜ ШҜШ§ШұШҜ ШЁЩҮ Ш§ЫҢЩҶ Щ…Ш№ЩҶЫҢ Ш§ШіШӘ Ъ©ЩҮ ШЁШ§ЫҢШҜ $t$ ЩҮШ§ЫҢ Щ…ШӘЩ…Ш§ЫҢШІ ШҜШұ ШҙШұШ§ЫҢШ· ШЁШҜШіШӘ ШўЩ…ШҜЩҮ Щ…Ш°Ъ©ЩҲШұ ШөШҜЩӮ Ъ©ЩҶЩҶШҜ. Ш№ШЁШ§ШұШӘ $k\left(\dfrac{\pi}{2^{10}}\right) $ ШұШ§ ШҜШұ ЩҶШёШұ ШЁЪҜЫҢШұЫҢШҜ ШЁЩҮ Ш§ЫҢЩҶ Щ…Ш№ЩҶЫҢ Ш§ШіШӘ Ъ©ЩҮ ШІЩҲШ§ЫҢЩҮ $\pi$ ШұШ§ ШЁЩҮ $2^{10}$ ЩӮШіЩ…ШӘ Щ…ШіШ§ЩҲЫҢ , ШӘЩӮШіЫҢЩ… Ъ©ШұШҜЫҢЩ….
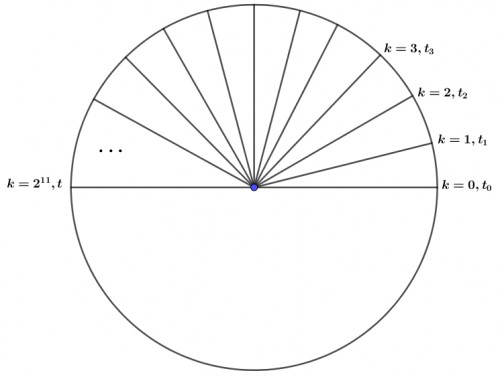
ЩҮЩ…Ш§ЩҶШ·ЩҲШұ Ъ©ЩҮ Щ…ШҙШ®Шө Ш§ШіШӘ ШЁШұШ§ЫҢ ЩҮШұ $0\leq k \leq 2^{10}$ ЫҢЪ© $t$ ЫҢЪ©ШӘШ§ЫҢЫҢ ШЁШҜШіШӘ Щ…ЫҢ ШўЫҢШҜ ЩҫШі ШЁЫҢШҙ Ш§ШІ ЩҮШІШ§Шұ $t$ ЩҲШ¬ЩҲШҜ ШҜШ§ШұШҜ. Ш§Щ…Ш§ Ш§ЪҜШұ ШЁШұШ§ЫҢ Щ…Ш«Ш§Щ„ $k=2^{11}$ Ш®ЩҲШ§ЩҮЫҢЩ… ШҜШ§ШҙШӘ $k\left(\dfrac{\pi}{2^{10}}\right) =2\pi$ Ъ©ЩҮ $2\pi$ ЩҮЩ…Ш§ЩҶ ШІШ§ЩҲЫҢЩҮ ШөЩҒШұ Ш§ШіШӘ Ъ©ЩҮ ЩӮШЁЩ„Ш§ Щ…ШӯШ§ШіШЁЩҮ Ъ©ШұШҜЫҢЩ… $(k=0,t_0)$ ЩҲ Ш¬ЩҲШ§ШЁ Щ…ШӘЩ…Ш§ЫҢШІЫҢ ЩҶЫҢШіШӘ. ЩҲ ЩҮЩ…ЫҢЩҶШ·ЩҲШұ ШЁШұШ§ЫҢ $k$ ЩҮШ§ЫҢЫҢ Ъ©ЩҮ Ш®Ш§ШұШ¬ Ш§ШІ Щ…ШӯШҜЩҲШҜЩҮ $0\leq k \leq 2^{10}$ Ш¬ЩҲШ§ШЁ Щ…ШӘЩ…Ш§ЫҢШІЫҢ ШЁШҜШіШӘ ЩҶЩ…ЫҢШ§ЫҢШҜ ШЁЩ„Ъ©ЩҮ Ш¬ЩҲШ§ШЁ ЩҮШ§ЫҢЫҢ ЩҮШіШӘЩҶШҜ Ъ©ЩҮ ЩӮШЁЩ„Ш§ Щ…ШӯШ§ШіШЁЩҮ Ъ©ШұШҜЫҢЩ…!