همانطور که میدانید دو خط در فضا یا باهم موازی هستند یا متقاطع و یا متنافر هستند.
برای تشخیص حالت ابتدا بردارهای دو خط را بدست می آوریم اگر $u=k u^{'} $ آنگاه دو خط موازی هستند که در آن $ u^{'} ,u $ بردارهای هادی خطوط و $ k $ عددی حقیقی است.(این شرط معادل است با اینکه اگر$ u=( p_{1} , q_{1} , r_{1} ) $ و $ u^{'} =( p_{2} , q_{2} , r_{2} ) $ آنگاه $ \frac{p_{1}}{p_{2}} = \frac{q_{1}}{q_{2}} = \frac{r_{1}}{r_{2}} $)
برای تشخیص متنافر یا متقاطع بودن دو روش داریم:
روش اول:
معدلات پارامتری یکی از خطوط را در معادلات پارامتری خط دیگر قرار میدهیم و با حل معادلات اگر جوابی بدست آید دو خط متقاطع هستند و با جایگذاری جواب در یکی از خطوط نقطه تقاطع بدست می آید اما اگر معادله جواب نداشته باشد دو خط متنافر هستند.
مثال:
وضعیت نسبی دو خط $L: \frac{x-1}{3} = \frac{y}{2} = \frac{z+1}{4} $ و$ \frac{x-2}{2} = \frac{y-5}{3} =z-3 $ را نسبت به هم بیابید؟
حل:
داریم: $ u=(3,2,4) $و$u^{'}=(2,3,1) $ اما $ \frac{3}{2} \neq \frac{2}{3} \neq \frac{4}{1} $پس موازی نیستند و معادله پارامتری خط $L $ یعنی $ \begin{cases}x=3t+1 \\y=2t\\z=4t-1\end{cases} $ را در معادله خط دوم قرار میدهیم یعنی داریم:
$$ \frac{3t-1}{2} =^{*} \frac{2t-5}{3} =^{**} 4t-4 $$
با حل رابطه ی $*$ جواب $ \frac{-7}{5} $ را داریم و با حل رابطه ی $**$ جواب $ \frac{7}{10} $
را داریم که برابر نیستند پس دو خط متنافر هستند.
روش دوم:
اگر $ u^{'} ,u $ بردارهای هادی دو خط $ l^{'} ,l$ باشند. نقطه ی دلخواه $ A $ را روی $ l $ و نقطه ای دیگر مانند $ B$ را روی $ l^{'} $ در نظر میگیریم اگر ضرب مختلط $ u^{'} ,u, \overrightarrow{AB} $ یعنی $\overrightarrow{AB}.(u^{'} \times u) $ صفر شود دو خط یا متقاطع هستند یا موازی اما اگر صفر نشود متنافر هستند.
مثال بالا را با این روش حل کنید:
$ u=(3,2,4) $و$ u^{'}=(2,3,1) $و$A=(1,0,-1) $و$B=(2,5,3) $و$ \overrightarrow{AB}=(1,5,4) $ یعنی داریم:
$$\overrightarrow{AB}.(u^{'} \times u)= \begin{vmatrix}1 & 5 & 4 \\3 & 2 & 4 \\2 & 3 & 1 \end{vmatrix} =47 \neq 0 $$
پس دو خط متنافر هستند.
(ساده ترین راه برای بدست آوردن یک نقطه از خط مساوی صفر قرار دادن صورت ها است)
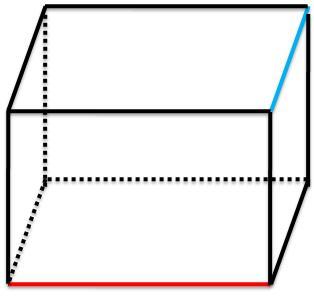
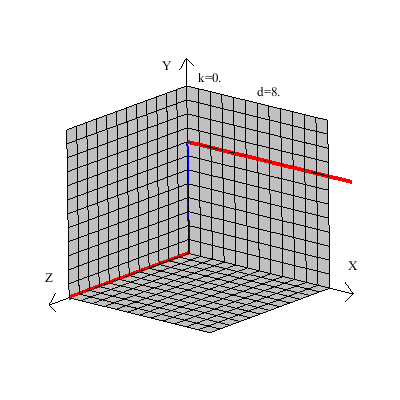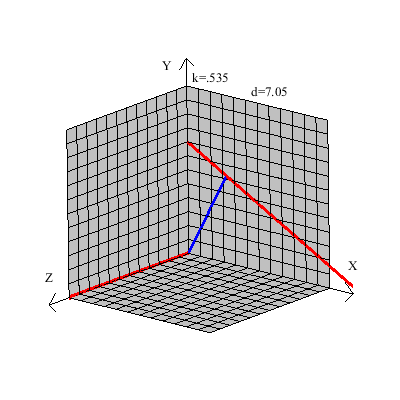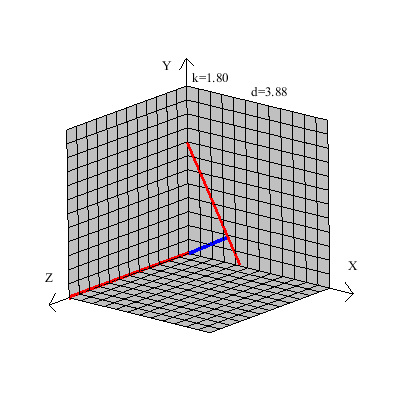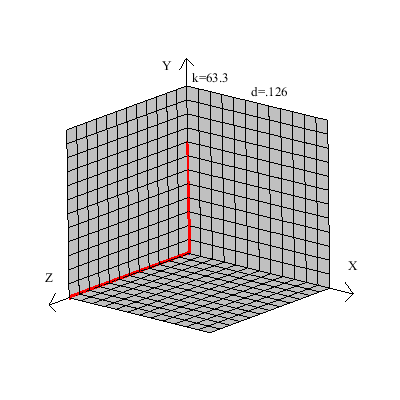
خط قرمز رنگ را در نظر بگیرید اگر صفحه زیرین مکعب را درب در نظر بگیریم و خط قرمز را لولا هر صفحه ای که شامل خط قرمز باشد از چرخش صفحه زیرین (درب) نسبت به این خط(خط لولا باشد) بدست می آید تمام این نوع صفحات نمیتوانند کل خط آبی را هم داخل خود داشته باشند( حداکثر در یک نقطه خط آبی را قطع میکنند)
یک شکل ساده از خطوط متنافر: