چطور جذر یک پاره خط رو با روش های هندسی به صورت دقیق پیدا کنیم؟

Question

می‌خواستم بدونم چطور می‌شه با روش‌های هندسی، ریشۀ دوم یک پاره‌خط رو پیدا کرد. نمی‌خوام از روش‌های پیدا کردن ریشۀ یک عدد براساس الگوریتم تکراری یا روش‌های دیگه‌ای که مقدار تقریبی رو می‌دهد پیش برم و روشی می‌خوام که طول دقیق ریشۀ دوم رو بهم بده.

Comments

@karimi6150 با سلام. صورت سؤال با متن سؤال ضدونقیض هستند. صورت سؤال مجذور پاره خط را میخواهد ولی متن سؤال جذر آن را!! لطفاً اصلاح نمایید. ضمناً دقیقترین نمایش جذر اعدادی که مربع کامل نیستند، شکل رادیکالی آنهاست و نمایش اعشاری نامتناهی دارند. با جستجوی عبارت «جذر پاره خط» در اینترنت، دو فایل ویدئویی در سایت aparat بطور کامل این مطلب را بصورت تصویری توضیح داده. دانلود و تماشای آن حتماً مفید خواهد بود. دانلود فایل pdf زیر نیز میتواند مفید واقع شود. با آرزوی موفقیت.
https://www.google.com/url?sa=t&source=web&rct=j&url=https://www.roshdmag.ir/Roshdmag_content/media/article/28.29%2520from%2520(95-96)%2520MATN%2520BORHAN%2520MOTEVASETE%25201%2520(%25207%2520)%252089-13_0.pdf&ved=2ahUKEwjh7qTn_qHuAhVzolwKHWYADycQFjADegQIAhAB&usg=AOvVaw2FDtHW6PjZ5FkIfVRtWBiT

---

ممنون آقای آهنگرپور از وقتی که گذاشتید و طبق تذکر به جای شما صورت سوال رو اصلاح کردم ٬ و معذرت میخوام از اینکه نتونستم سوالم رو اونجور که انتظار جواب دارم مطرح بکنم.
راه حل‌هایی رو که آدرس دادید قبلاً امتحان کرده بودم و توی اونها یا باید یکسری عملیاتها رو به صورت متوالی انجام داد تا به جواب رسید یا با آگاهی از مربع‌های کامل نزدیک به اون عدد پیش رفت ولی اون چیزی که من میخوام اینه که به عنوان مثال جذر خطی به طول  127/6666666 را فقط با خط‌کش و پرگار بدون اینکه دقیقاً بدونیم طول خط چقدره روی اون مشخص کنیم (صد البته تنها چیزی که باید بدونیم واحد اندازه‌گیری خطه ٬ مثلاً یک اینچ باشه که جذرش بشه خودش یا 25.4 میلیمتر که بشه 5.04 ) و یک راه‌حل کلی برای هر خط دیگه‌ای با هر طول داشته باشیم. مثل کاری که برای پیدا کردن نقطه وسط یک پاره خط یا نیمساز یک زاویه انجام میدیم بدون اینکه طول خط یا اندازه زاویه مهم باشه میشه با خط‌کش و پرگار به دست آورد.
حتی اگه کسی بتونه با اطمینان بگه که هیچ راه‌حلی تا حالا برای اینکار کشف نشده هم من به جوابم رسیده‌ام.

Answer 1

سلام خدمت شما دوست عزیز اگر شما پاره خطّی به اندازۀ $a$ داشته باشید،می توانید پاره خط $ \sqrt{a} $را دقیق و بدون نقص رسم کنید.برای این کار می توانید از یک قضیه در مثلّث قائم الزّاویه استقاده کنید.

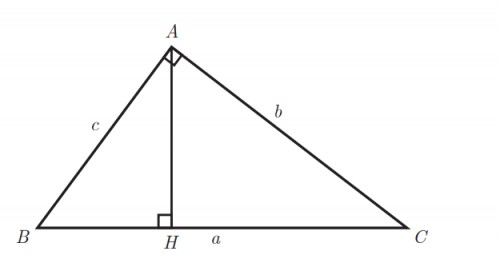
این قضیه بیان می کند اگر$AH$ ارتفاع وارد بر وتر باشد،توان دوم ارتفاع برابر است با حاصل ضرب قطعه هایی که روی وتر ایجاد می کند یعنی $AH^{2} $$BH.CH=$

حال اگر ما یکی از پاره خط های وتر مثلا$CH$را برابر با$a$و دیگری را برابر با 1 واحد در نظر بگیریم و ارتفاع مثلّث قائم الزّاویه را رسم کنیم،به طور حتم برابر با $ \sqrt{a} $می شود.

Comments

ممنون آقا/خانم mmvf دقیقا دنبال چنین چیزی بودم و پیرو پاسخ شما پس میتونیم از روش عکس زیر هم استفاده کنیم که خیلی روش ساده‌ای میشه و عجیبه که در همه سایتها راه‌حلهای طولانی برای اینکار ذکر شده و چنین راه‌حل ساده و دم‌دستی رو مطرح نکردند.![توضیحات تصویر][1]


  [1]: https://math.irancircle.com/?qa=blob&qa_blobid=6534489901774750544

---

@karimi6150 با درود مجدد. روشی که با عکس مذکور در دیدگاهتان درج کردید، روش بهتری است. چون انتخاب اندازه پاره خطی که جذرش مطلوب شماست، در اختیار خودتان است. علت این امر این است که شما از هر نقطه روی قطر نیمدایره عمود بر نیمدایره رسم کنید و تقاطع آن با نیمدایره را به دوسر قطر نیمدایره وصل کنید، مثلثی قائم الزاویه خواهید داشت که با پاسخ صحیح کاربر گرامی @mmvf همخوانی دارد. این روش ساده در کتاب معتبر زیر هم آمده است.
Number, Shape, & Symmetry_ An Introduction to Number Theory, Geometry, and Group Theory, Diane L. Herrmann, Paul J. Sally, Jr., 2013, CRC Press, P:380-381
لینک زیر را با جستجوی عبارت «how to construct the square root of a segment» بدست آوردم که همین روش ساده را توضیح داده است. با آرزوی موفقیت.
https://math.stackexchange.com/questions/705/compass-and-straightedge-construction-of-the-square-root-of-a-given-line