بیشترین مقدار تابع $y= \frac{16x }{(4+x)^2} $ را بیابید.

Question

بیشترین مقدار تابع $y= \frac{16x }{(4+x)^2} $ رو چطوری بدست بیارم ؟ از طریق مشتق حل میشه ؟ بعد از مشتق گیری چی کار کنم ؟

Comments

Lotus@ تایپ ریاضی که در سایت آمده را مطالعه کنید و مانند نمونه عمل کنید.

Answer 1

$y'= \frac{16-x^2}{(x+4)^2}=0 \Rightarrow x= \mp 4 $

4- که عضو دامنه نیست

$$\begin{array}{l|c|r} x&-\infty \quad-4 \quad \quad 4 \quad+ \infty \\ \hline y'&\quad\quad-\quad\quad|| \quad+0\quad-\quad \quad \\ \hline y&0\quad\quad\quad|| \quad\quad1\quad \quad 0\\ \end{array}$$

به این ترتیب در نقطه $(4,1)$ یک ماکسیمم نسبی و مطلق دارد

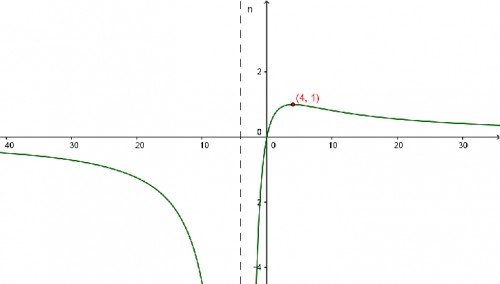
و بیشترین مقدار این تابع 1 خواهد بود.