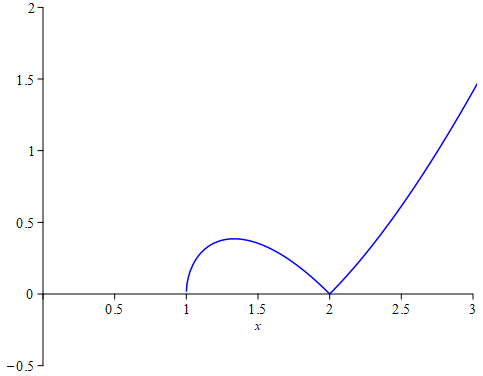
ШӘЩҲШ¬ЩҮ Ъ©ЩҶЫҢШҜ Ъ©ЩҮ ЪҜЩҲШҙЩҮЩ” ШӘЫҢШІ ШҜШұ ШұШіЩ… ЩҶЩ…ЩҲШҜШ§Шұ Ш§ЫҢЩҶ ШӘШ§ШЁШ№ ШҜШұ ЩҶЩӮШ·ЩҮЩ” $x=2$ Ъ©ЩҮ ЩӮШҜШұЩ…Ш·Щ„ЩӮ ЩҫШҙШӘ Ш№ШЁШ§ШұШӘ ШұШ§ШҜЫҢЪ©Ш§Щ„ЫҢвҖҢШӘШ§ЩҶ Ш§ШіШӘ Ш§ЫҢШ¬Ш§ШҜ Щ…ЫҢвҖҢШҙЩҲШҜ ЩҲ Ш§Щ„ШЁШӘЩҮ ШЁЩҮ ШҙШұШ· Ш§ЫҢЩҶЪ©ЩҮ ЫІ Ш§ШІ $-a$ ШЁШІШұЪҜШӘШұ ШЁШ§ШҙШҜ ЪҶЩҲЩҶ ШҜШ§Щ…ЩҶЩҮЩ” ШӘШ§ШЁШ№вҖҢШӘШ§ЩҶ $[-a,+\infty)$ Ш§ШіШӘ. ЩҶЩ…ЩҲШҜШ§Шұ ШӘШ§ШЁШ№вҖҢШӘШ§ЩҶ ШҙШЁЫҢЩҮ Ш®Щ… ШўШЁЫҢвҖҢШұЩҶЪҜ ШҜШұ ШҙЪ©Щ„ ШІЫҢШұ Щ…ЫҢвҖҢШҙЩҲШҜ. ЩҲ ШҜЩҲ Ш®Ш·Щҗ Щ…Щ…Ш§Ші ШЁШұ ШӘШ§ШЁШ№ ШҜШұ Ш§ЫҢЩҶ ЩҶЩӮШ·ЩҮ ШЁШ§ ШұЩҶЪҜ ЩӮШұЩ…ШІ ЩҶШҙШ§ЩҶ ШҜШ§ШҜЩҮвҖҢШҙШҜЩҮвҖҢШ§ЩҶШҜ.
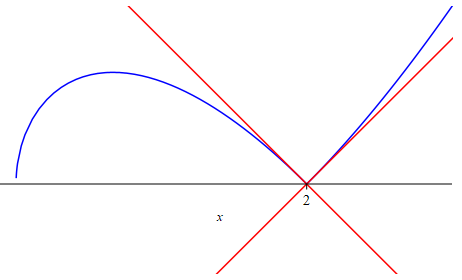
ШӘЩҲШ¬ЩҮ Ъ©ЩҶЫҢШҜ Ъ©ЩҮ ШҙЫҢШЁ Ш®Ш·ЫҢ Ъ©ЩҮ Ш§ШІ ШіЩ…ШӘЩҗ ЪҶЩҫ Щ…Щ…Ш§Ші Ш§ШіШӘ ШЁШұШ§ШЁШұ ШЁШ§ Щ…ЩӮШҜШ§ШұЩҗ Щ…ШҙШӘЩӮЩҗ ЪҶЩҫ ШӘШ§ШЁШ№ ШҜШұ $x=2$ ЩҲ ШҙЫҢШЁ Ш®Ш· Щ…Щ…Ш§Ші Ш§ШІ ШіЩ…ШӘ ШұШ§ШіШӘ ШЁШұШ§ШЁШұ ШЁШ§ Щ…ЩӮШҜШ§Шұ Щ…ШҙШӘЩӮЩҗ ШұШ§ШіШӘ ШӘШ§ШЁШ№ ШҜШұ $x=2$ Ш§ШіШӘ. ШЁШұШ§ЫҢ ШЁШҜШіШӘ ШўЩҲШұШҜЩҶ Щ…ШҙШӘЩӮ ЪҶЩҫ ЩҲ ШұШ§ШіШӘ ЩҮЩ… ШӘЩҲШ¬ЩҮ Ъ©ЩҶЫҢШҜ Ъ©ЩҮ ШӘШ§ШЁШ№ ШҙЩ…Ш§ ШҜШұ ШіЩ…ШӘ ЪҶЩҫ ШЁШұШ§ШЁШұ ШЁШ§ $-(x-2)\sqrt{x+a}$ ЩҲ ШҜШұ ШіЩ…ШӘ ШұШ§ШіШӘ ШЁШұШ§ШЁШұ ШЁШ§ $(x-2)\sqrt{x+a}$ Ш§ШіШӘ. ШІШ§ЩҲЫҢЩҮвҖҢШ§ЫҢ Ъ©ЩҮ Ш§ШІ ШўЩҶ ШӯШұЩҒ Щ…ЫҢвҖҢШІЩҶЫҢШҜ ШІШ§ЩҲЫҢЩҮЩ” ШЁШ§Щ„Ш§ЫҢЩҗ ШЁЫҢЩҶ ШҜЩҲ Ш®Ш· ЩӮШұЩ…ШІ Ш§ШіШӘ. Ш§ЫҢЩҶ ШІШ§ЩҲЫҢЩҮ ШұШ§ $\alpha$ ШЁЩҶШ§Щ…ЫҢШҜ. ШІШ§ЩҲЫҢЩҮЩ” Щ…Ъ©Щ…Щ„Щҗ ШўЩҶ ЩҶШіШЁШӘ ШЁЩҮ Ш®Ш· Щ…Щ…Ш§Ші ШіЩ…ШӘ ЪҶЩҫ ШұШ§ $\beta$ ШЁЩҶШ§Щ…ЫҢШҜ. ШӘЩҲШ¬ЩҮ Ъ©ЩҶЫҢШҜ Ъ©ЩҮ ЪҶЩҲЩҶ Щ…ЩӮШҜШ§Шұ Щ…ШҙШӘЩӮ ЪҶЩҫ ЩҲ ШұШ§ШіШӘ ЩҒЩӮШ· ЩӮШұЫҢЩҶЩҮЩ” ЫҢЪ©ШҜЫҢЪҜШұ ЩҮШіШӘЩҶШҜ (ЫҢЪ©ЫҢ Щ…ЩҶЩҒЫҢЩҗ ЫҢЪ© ШЁШұШ§ШЁШұЩҗ ШҜЫҢЪҜШұЫҢ Ш§ШіШӘ) ЩҫШі Ш§ЩҶШҜШ§ШІЩҮЩ” ШІШ§ЩҲЫҢЩҮЩ” ШЁЫҢЩҶ Ш®Ш· Щ…Щ…Ш§Ші ЪҶЩҫ ЩҲ Щ…ШӯЩҲШұ $x$ЩҮШ§ ШЁШұШ§ШЁШұ ШЁШ§ Ш§ЩҶШҜШ§ШІЩҮЩ” ШІШ§ЩҲЫҢЩҮЩ” ШЁЫҢЩҶ Ш®Ш· Щ…Щ…Ш§Ші ШұШ§ШіШӘ ЩҲ Щ…ШӯЩҲШұ $x$ЩҮШ§ Ш§ШіШӘШҢ ШӘЩҶЩҮШ§ ЫҢЪ©ЫҢ ШіШ§Ш№ШӘЪҜШұШҜ ЩҲ ЫҢЪ©ЫҢ ЩҫШ§ШҜШіШ§Ш№ШӘЪҜШұШҜ ЩҶШіШЁШӘ ШЁЩҮ Щ…ШӯЩҲШұ $x$ЩҮШ§ Ш§ШіШӘ. ЩҫШі Ш§ЪҜШұ ШІШ§ЩҲЫҢЩҮЩ” ШЁЫҢЩҶ Щ…ШӯЩҲШұ $x$ЩҮШ§ (Ш®Ш· ШіЫҢШ§ЩҮвҖҢШұЩҶЪҜ) ЩҲ Ш®Ш· ЩӮШұЩ…ШІ Щ…Щ…Ш§Ші ШұШ§ШіШӘ (ШұЩҲ ШЁЩҮ ШұШ§ШіШӘ) ШұШ§ $\theta$ ШЁЩҶШ§Щ…ЫҢЩ… ШўЩҶЪҜШ§ЩҮ ШҜШ§ШұЫҢЩ…:
\begin{align}
\theta &= \arctan(m)\\
\beta &= 2\theta\\
\alpha &= \pi -\beta
\end{align}
Ъ©ЩҮ $m$ ШҙЫҢШЁ Ш®Ш· Щ…Щ…Ш§Ші ШұШ§ШіШӘ Ш§ШіШӘ ЫҢШ№ЩҶЫҢ
\begin{align}
m &= f'_+|_{x=2}\\
&= \Big(\big((x-2)\sqrt{x+a}\big)'_x\Big)|_{x=2}\\
&= \big(\sqrt{x+a}+(x-2)\frac{1}{2\sqrt{x+a}}\big)|_{x=2}\\
&= \sqrt{a+2}
\end{align}
Ш§Ъ©ЩҶЩҲЩҶ ЩҒШұШ¶ ЩҫШұШіШҙ Ъ©ЩҮ $\alpha=\frac{\pi}{2}$ Ш§ШіШӘ ШұШ§ ШЁЩҮ Ъ©Ш§Шұ Щ…ЫҢвҖҢЪҜЫҢШұЫҢЩ…. ШҜШ§ШұЫҢЩ… $\beta=\pi-\frac{\pi}{2}=\frac{\pi}{2}$ШҢ ЩҫШі $\theta=\frac{\frac{\pi}{2}}{2}=\frac{\pi}{4}$ШҢ ЩҲ ШҜШұ ЩҫШ§ЫҢШ§ЩҶ $m=\tan\frac{\pi}{4}=1$ ЩҫШі $\sqrt{a+2}=1$ ЩҲ $a+2=1$ ЩҲ $a=-1$. Ш§Ъ©ЩҶЩҲЩҶ ШҙЪ©Щ„ ЩҶЩ…ЩҲШҜШ§ШұЩҗ Щ…ЩҲШұШҜ ЩҶШёШұ ШұШ§ ШІЩ…Ш§ЩҶЫҢ Ъ©ЩҮ $a=-1$ ШұШ§ ЩҶЪҜШ§ЩҮ Ъ©ЩҶЫҢШҜ. ШҜШіШӘЩҲШұЩҗ Ъ©ШҙЫҢШҜЩҶЩҗ ШўЩҶ ШЁШ§ ЩҶШұЩ…вҖҢШ§ЩҒШІШ§Шұ Щ…ЫҢЩҫЩ„ ШҜШұ ШІЫҢШұ ШўЩ…ШҜЩҮвҖҢШ§ШіШӘ.
plot(abs(x-2)*sqrt(x-1), x=0..4, color=blue, view=[0..3, -0.5..2], scaling=constrained, tickmarks=[10,5]);