در ذوزنقهٔ $ABCD$ دو یال $AB$ و $CD$ موازی هستند. پاره خط $EF$ را موازی آنها رسم کنید. ثابت کنید $EF=\frac{ED.AB+AE.DC}{AD}$.

Question

در ذوزنقهٔ زیر داریم $ AB\mid EF\mid CD$، یعنی $AB$ و $EF$ و $CD$ موازی هستند. و همینطور داریم $AE=m$ و $ED=n$ و $AB=a$ و $CD=b$. اکنون ثابت کنید که $EF=\frac{na+mb}{m+n}$.

Comments

@pipa لطفا عنوان سوال را اصلاح کنید

---

@pipa پست زیر را بخوانید. گذاشتن عنوان مناسب مهم است. https://math.irancircle.com/11973 عنوان پیشین‌تان «اثبات این رو کسی می تونه انجام بده» را با عنوان جدیدی که برایتان در ویرایش گذاشتم مقایسه کنید. اگر پرسش با عنوان شبیه به عنوان قبلی‌تان بفرستید بهتر است پرسش‌تان بسته شود تا اینکه پاسخ داده‌شود.

Answer 1

• از $A$ موازی $BC$ رسم می‌کنم.

• چهارضلعی $ABFG$ متوازی‌اضلاع است پس

$$EF=x+a$$

• با استفاده قضیه تالس داریم

$$ \frac{m}{n+m} = \frac{x}{b-a} \Rightarrow x= \frac{m(b-a) }{m+n}$$

• بنابراین $$EF= \frac{na+mb}{m+n}$$

Answer 2

ضلع های $AD$ و $BC$ را ادامه می دهیم تا همدیگر را در نقطه $M$ قطع کنند . فرض کنید $EF = x$ و $AM = y$ . شکل زیر را خواهیم داشت :

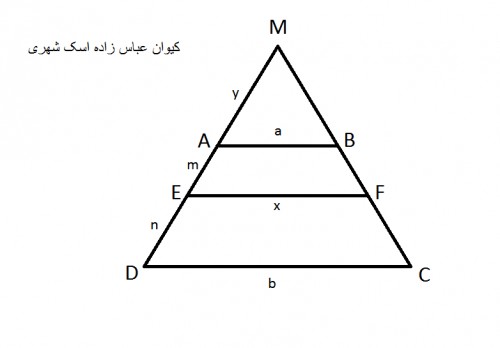
چون $AB \| DC$ پس طبق قضیه تالس داریم :

$$ \frac{AM}{DM} = \frac{AB}{DC} $$

یعنی :

$$ \frac{y}{y + m + n} = \frac{a}{b} $$

بعد از طرفین - وسطین مقدار $y$ عبارتست از :

$$y = \frac{ma + na}{b - a} \ \ \ \clubsuit $$

از طرفی $AB \| EF$ پس طبق قضیه تالس داریم :

$$ \frac{AM}{EM} = \frac{AB}{EF} $$

یعنی :

$$ \frac{y}{y + m} = \frac{a}{x} \ \ \ \ \spadesuit $$

حال با توجه به $ \clubsuit $ مقدار $y$ را در تساوی $ \spadesuit $ جاگذاری می کنیم که خواهیم داشت :

$$ \frac{ \frac{ma + na}{b-a} }{ \frac{ma + na}{b-a} + m} = \frac{a}{x} $$

بعد از طرفین - وسطین مقدار $x$ عبارتست از :

$$x = \frac{na + mb}{m + n} $$

پس :

$$EF = \frac{na + mb}{m + n}$$

Answer 3

به نام خدا.

از $A$ به $D$ وصل کنید. شکل زیر

نقطه $G$ تقاطع $EF$ با $AD$ است. می‌دانیم که $ \frac{AE}{CE}= \frac{m}{n} = \frac{BF}{DF} \Longrightarrow \frac{DF}{BF+DF} = \frac{n}{m+n} $

حال در مثلث $ADC$ داریم:

$ \frac{m}{m+n} = \frac{EG}{CD} \Longrightarrow EG= \frac{CD×m}{m+n}= \frac{bm}{m+n} $

و‌ در مثلث $ABD$ داریم:

$ \frac{GF}{a} = \frac{DF}{DF+BF} = \frac{n}{m+n} \Longrightarrow GF= \frac{an}{m+n} $

پس طول $EF$ می‌شود:

$EF=EG+FG= \frac{bm}{m+n} + \frac{an}{m+n} = \frac{bm+an}{m+n} $