برای کشیدن یک بیضیگون که سه محورش دقیقا سه محور مختصات هستند و مرکزش مرکز مختصات که با برابریِ $\frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}=1$ داده میشود کافیست نقطههای زیر را بردارید که همارز با نشانهزدنِ $a$ و $b$ و $c$ به ترتیب روی محورهای $x$ها و $y$ها و $z$ها و همینطور قرینههایشان است.
$$\lbrace (\pm a,0,0),(0,\pm b,0),(0,0,\pm c)\rbrace$$
در زیر برای حالت پرسش شما کشیده شده است.
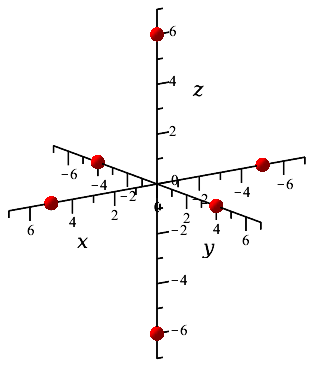
سپس سه بیضیای که از قطعدادنِ بیضیگون با صفحههای مختصات بدست میآید را بکشید تا حسی از بیضیگون را رساندهباشید. توجه کنید که یک بیضیگون برابر با اجتماع سه بیضیِ دو بعدی نیست! بلکه این سه بیضیِ دو بعدی زیرمجموعهای از این رویهٔ سهبعدی هستند! در زیر این سه بیضی را میبینید.
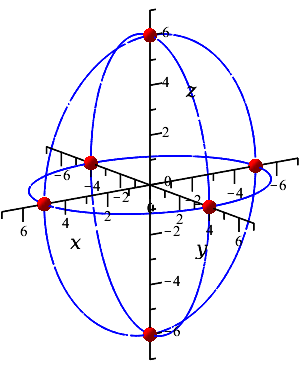
اما خود بیضیگون را نیز در شکل زیر افزودهایم.
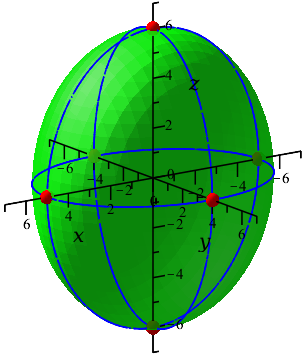
کشیدن اینها با دست کاری ندارد، ولی اگر دستور کشیدن آنها با نرمافزار Maple را هم خواستید در زیر آوردهایم.
f:=x^2/25+y^2/16+z^2/36-1:
points:=[[5,0,0],[-5,0,0],[0,4,0],[0,-4,0],[0,0,6],[0,0,-6]]:
pPoints:=plot3d(points,style=point,symbol=solidsphere,symbolsize=20,color=red):
pView:=[-7..7,-7..7,-7..7]:
plots:-display(pPoints,view=pView,axes=normal,labels=[x,y,z],labelfont=[Times,16]);
ellipses:=[seq(eval(f,[var=0]),var in [z,y,x])]:
var:=[x,y,z]:
pEllipses:=[seq(plots:-intersectplot(ellipses[i]=0,var[4-i]=0,x=-7..7,y=-7..7,z=-7..7,color=blue),i=1..3)]:
plots:-display(pPoints,seq(j,j in pEllipses),view=pView,axes=normal,labels=[x,y,z],labelfont=[Times,16]);
pEllipsoid:=plots:-implicitplot3d(f=0,x=-7..7,y=-7..7,z=-7..7,color=green,transparency=0.2,style=surface):
plots:-display(pPoints,seq(j,j in pEllipses),pEllipsoid,view=pView,axes=normal,labels=[x,y,z],labelfont=[Times,16]);