دو بازتاب متوالی در این مستطیل روی دو ضلع غیر یکسان صورت میگیرد که یا مجاورند و یا مقابل؛ و با توجه به تصویر زیر میتوان ثابت کرد که در هر دو صورت مسیر نور پس از دو بازتاب متوالی موازی است:
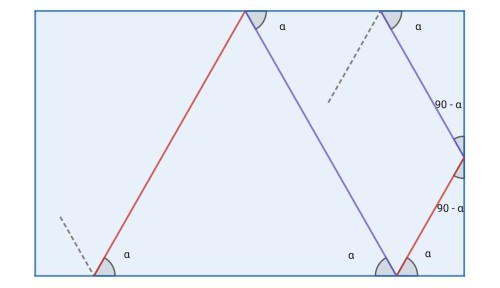
بنابراین هر نمونه از این مسیر حداکثر شامل دو شیب برای خطوط مسیر میباشد. با توجه به گزینه های موجود نور تنها میتواند با شیبی که وارد شده است خارج بشود.
حال فرض کنید نمونه ای داریم که در آن نور از نقطه بالا سمت چپ مستطیل وارد شده و از نقطه پایین سمت راست خارج میشود. در این صورت اگر تصویر حاصل شده را $180°$ دوران دهیم به همان تصویر اولیه میرسیم زیرا نور با همان شرایط یکسان (یعنی از همان نقطه بالا سمت چپ و همان شیب اولیه) وارد شده است. از این موضوع میتوان نتیجه گرفت که هر الگویی که در آن نور از نقطه ای وارد و از نقطه ای غیرمجاور خارج میشود دارای تقارن مرکزی است و از آنجا که تقارن مرکزی در مورد مستطیل نیز باید صدق کند پس مرکز تقارن مرکز مستطیل است.

هم اکنون بیاید فرض کنیم در این نمونه نور به صورت همزمان از نقطه بالا سمت چپ و پایین سمت راست وارد مستطیل میشود. این دو مسیر دقیقا در یک نقطه به یکدیگر میرسند (منظور قطع کردن نیست بلکه منظور نقطه ایست که پس از آن هریک مسیر دیگری را ادامه میدهد). در حقیقت مسیری که نور ورودی از نقطه پایین سمت راست طی میکند همان قرینه مسیر نور ورودی از نقطه بالا سمت چپ نسبت به مرکز مستطیل است و زمانی که این دو به هم میرسند نقطه ای داریم که خودش و قرینه اش نسبت به مرکز مستطیل منطبق شده اند بنابراین نقطه مورد نظر مرکز مستطیل است و این نشان میدهد که حکم احتمالا درست است (توجه داشته باشید که این اثبات از لحاظ ریاضی کامل نیست و صرفا در توصیف و ایجاد ذهنیت کلی به ما کمک میکند)