ارتفاع مثلث ABC را رسم می کنیم تا BC را در H قطع کند. و در مثلث ACP و ABP ارتفاع PQ و PZ را به صورت شکل زیر رسم می کنیم.
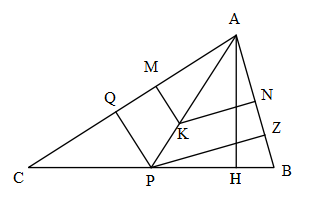
مساحت مثلث APC برابر است با:
1/2.AH.CP
مساحت مثلث ABP برابر است با:
1/2.AH.BP
از آنجایی که AP میانه است پس CP=BP است پس مساحت دو مثلث ACP با ABP مساوی است.
چون PQ ارتفاع مثلث ACP است؛ مساحت ACP برابر است با:
1/2.PQ.AC
چون PZ ارتفاع مثلث ABP است؛ مساحت ABP برابر است با:
1/2.PZ.AB
از آنجایی که نتیجه گرفتیم مساحت این دو مثلث برابر است پس داریم:
1/2.PQ.AC = 1/2.PZ.AB
دو طرف رابطه بالا را در 2 ضرب میکنیم:
PQ.AC = PZ.AB
حال دو طرف را در یک بر روی PZ ضرب می کنیم:
PQ.AC/PZ=AB
حال دو طرف را در یک بر روی AC ضرب می کنیم؛ نتیجه میگیریم که:
رابطه 1
PQ/PZ=AB/AC
در مثلث AQP نسبت به دو متوازی KM و PQ داریم:
رابطه 2
KM/PQ = AK/AP
در مثلث AZP نسبت به دو متوازی KN و PZ داریم:
رابطه 3
KN/PZ = AK/AP
از رابطه 2 و 3 نتیجه می گیریم:
رابطه 4
KM/PQ = KN/PZ = AK/AP
رابطه زیر از رابطه 4 گرفته شده:
KM/PQ = KN/PZ
دو طرف را در یک بر روی KM ضرب می کنیم:
KN/PZ.KM = 1/PQ
حال دو طرف را در PZ ضرب می کنیم:
رابطه 5
PZ/PQ = KN/KM
بنا بر رابطه 1 نتیجه می گیریم:
رابطه 6
PZ/PQ = AC/AB
بنا بر رابطه 6 و 5 به حکم می رسیم پس:
KN/KM = AC/AB