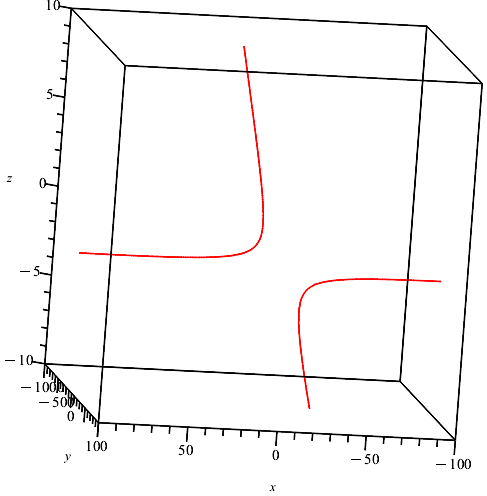
ШІЩ…Ш§ЩҶЫҢ Ъ©ЩҮ ШҜЩҲ ШЁШұШ§ШЁШұЫҢ ЩҲЩ„ЫҢ ШіЩҮ Щ…Ш¬ЩҮЩҲЩ„ ШҜШ§ШұЫҢШҜШҢ ЩҶШЁШ§ЫҢШҜ Ш§ЩҶШӘШёШ§Шұ ШҜШ§ШҙШӘЩҮвҖҢШЁШ§ШҙЫҢШҜ Ъ©ЩҮ ШӯШӘЩ…Ш§ ЩҒЩӮШ· ШЁЩҮ ЫҢЪ© ЩҫШ§ШіШ® ЫҢЪ©ШӘШ§ШҢ ЫҢЪ© ЩҶЩӮШ·ЩҮШҢ ШЁШұШіЫҢШҜ. Щ…Ш¬Щ…ЩҲШ№ЩҮ ЩҫШ§ШіШ®вҖҢЩҮШ§ЫҢ $x+y-z^2=0$ ЫҢЪ© ШұЩҲЫҢЩҮЩ” ШҜЩҲШЁШ№ШҜЫҢ ШҙШЁЫҢЩҮ ШЁЩҮ ШіЩҮЩ…ЫҢвҖҢЪҜЩҲЩҶ Щ…ЫҢвҖҢШҙЩҲШҜ. ШҙЪ©Щ„ ШІЫҢШұ ШұШ§ ШЁШЁЫҢЩҶЫҢШҜ.
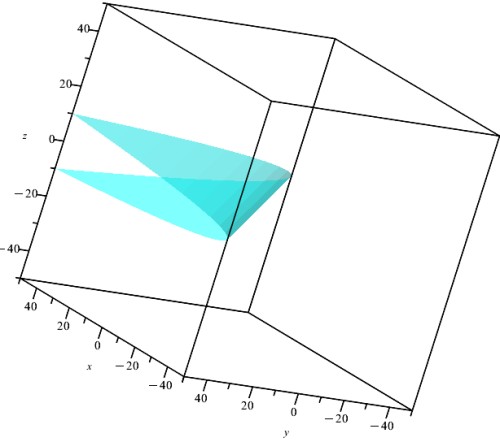
Щ…Ш¬Щ…ЩҲШ№ЩҮ ЩҫШ§ШіШ®вҖҢЩҮШ§ЫҢ $12y-5xz=0$ ШЁШ§ ШҙШұШ·Щҗ $y,z\neq 0$ ЩҶЫҢШІ ШЁШұШ§ШЁШұ ШЁШ§ ШұЩҲЫҢЩҮЩ” ШҜЩҲШЁШ№ШҜЫҢ ШҜШұ ШҙЪ©Щ„ ШІЫҢШұ Ш§ШіШӘ Ъ©ЩҮ ЫҢЪ© ЩҶЩӮШ·ЩҮ (Щ…ШЁШҜШЈ) ШұШ§ Ш§ШІ ШўЩҶ ШЁШұШҜШ§ШҙШӘЩҮвҖҢШЁШ§ШҙЫҢШҜ.
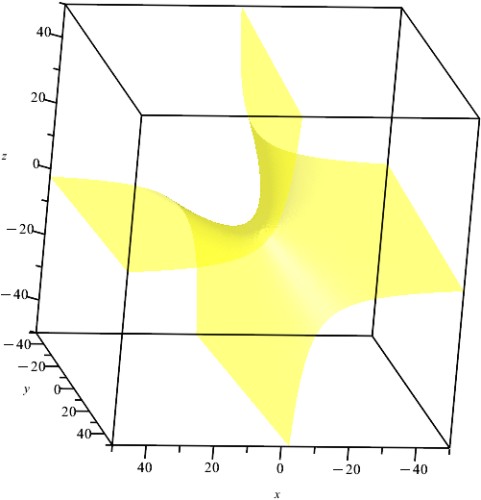
Ш§Ъ©ЩҶЩҲЩҶ Щ…Ш¬Щ…ЩҲШ№ЩҮ ЩҫШ§ШіШ®вҖҢЩҮШ§ЫҢ ШҜШіШӘЪҜШ§ЩҮ ШҜЩҲ ШЁШұШ§ШЁШұЫҢ-ШіЩҮвҖҢ Щ…Ш¬ЩҮЩҲЩ„ЫҢвҖҢШӘШ§ЩҶ ШЁШұШ§ШЁШұ ШЁШ§ Ш§ШҙШӘШұШ§Ъ© Ш§ЫҢЩҶ ШҜЩҲ ШұЩҲЫҢЩҮ Ш§ШіШӘ Ъ©ЩҮ ЫҢЪ© ЩҶЩӮШ·ЩҮ ЩҶЩ…ЫҢвҖҢШҙЩҲШҜШҢ ШЁЩ„Ъ©ЩҮ ЫҢЪ© Ш®Щ… ЩҶШ§ЩҮЩ…ШЁЩҶШҜ (ШҜЩҲ Ш®Щ… ЩҮЩ…ШЁЩҶШҜ) ШІЫҢШұ Щ…ЫҢвҖҢШҙЩҲШҜ.
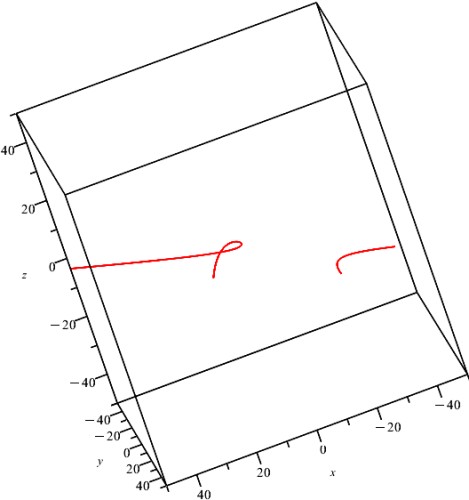
Ш§ЪҜШұ ШҜЩҲШіШӘ ШҜШ§ШұЫҢШҜ Ш§ЫҢЩҶ Ш§ШҙШӘШұШ§Ъ© ШұШ§ ШЁЩҮШӘШұ ШЁШЁЫҢЩҶШҜЫҢ Щ…ЫҢвҖҢШӘЩҲШ§ЩҶЫҢШҜ ШҜЩҲ ШұЩҲЫҢЩҮ ШұШ§ ШЁШ§ ЩҮЩ… ЩҶЩ…Ш§ЫҢШҙ ШҜЩҮЫҢШҜ.
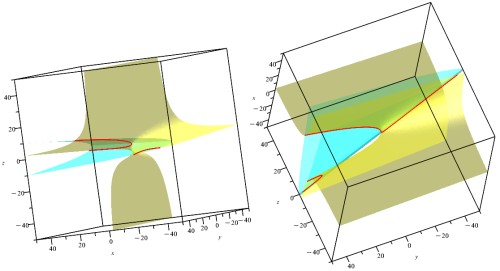
ЩҫШі ЩҶЩ…ЫҢвҖҢШӘЩҲШ§ЩҶЫҢШҜ ШЁЪҜЩҲШҰЩҠШҜ В«$z$ ЪҶЩҶШҜ Ш§ШіШӘШҹВ» ШІЩ…Ш§ЩҶЫҢ Щ…ЫҢвҖҢШӘЩҲШ§ЩҶЫҢШҜ Ш§ЫҢЩҶ ШұШ§ ШЁЪҜЩҲШҰЫҢШҜ Ъ©ЩҮ ШӘЩҶЩҮШ§ ЫҢЪ© Щ…ЩӮШҜШ§Шұ ШЁШұШ§ЫҢ $z$ Щ…Щ…Ъ©ЩҶ ШЁШ§ШҙШҜ. Ш«Ш§ШЁШӘ Щ…ЫҢвҖҢЪ©ЩҶЫҢЩ… Ъ©ЩҮ $z$ ЩҮШұ Щ…ЩӮШҜШ§ШұЫҢ ШЁЩҮ Ш¬ШІ ШөЩҒШұ Щ…ЫҢвҖҢШӘЩҲШ§ЩҶШҜ ШЁШ§ШҙШҜ. Ш№Щ„ШӘ ШӯШ°ЩҒ Ъ©ШұШҜЩҶЩҗ ШөЩҒШұ ШҜШұ Щ…Ш®ШұШ¬ ШЁЩҲШҜЩҶ ШҜШұ ШЁШұШ§ШЁШұЫҢЩҗ ШҜЩҲЩ… ШҜШіШӘЪҜШ§ЩҮ Ш§ШіШӘ. Ш§Щ…Ш§ ЪҶШұШ§ ЩҮШұ Щ…ЩӮШҜШ§Шұ ШҜЫҢЪҜШұЫҢ Щ…ЫҢвҖҢШӘЩҲШ§ЩҶШҜ ШЁШ§ШҙШҜШҹ ШӘЩҲШ¬ЩҮ Ъ©ЩҶЫҢШҜ Ъ©ЩҮ Ш§ШІ ЫҢЪ© ШҙЪ©Щ„ Ъ©ЩҮ ШҜШұ ЩҶШ§ШӯЫҢЩҮЩ” Щ…ШӯШҜЩҲШҜЫҢ Ъ©ШҙЫҢШҜЩҮ ШҙШҜЩҮвҖҢШ§ШіШӘ ЩҶЩ…ЫҢвҖҢШӘЩҲШ§ЩҶ ЩҶШӘЫҢШ¬ЩҮ ШҜШұ Щ…ЩҲШұШҜ Ъ©Щ„ ЩҒШ¶Ш§ЫҢ ШЁЫҢЪ©ШұШ§ЩҶ ЪҜШұЩҒШӘШҢ ШЁЩ„Ъ©ЩҮ ШӘЩҶЩҮШ§ Щ…ЫҢвҖҢШӘЩҲШ§ЩҶ Ш§ЫҢШҜЩҮ ЪҜШұЩҒШӘ. ШЁЩҮ ЩҮШұ ШӯШ§Щ„ ШІЩ…Ш§ЩҶЫҢ Ъ©ЩҮ ШҜЩҲ ШЁШұШ§ШЁШұЫҢ ШұШ§ ШіШ§ШҜЩҮ ЩҲ $y$ ШұШ§ ШӯШ°ЩҒ Щ…ЫҢвҖҢЪ©ЩҶЫҢЩ… ШЁЩҮ $x+\frac{5}{12}xz-z^2=0$ Щ…ЫҢвҖҢШұШіЫҢЩ…. Ш§ЫҢЩҶ ЫҢЪ© ШЁШұШ§ШЁШұЫҢЩҗ ШҜШұШ¬ЩҮ ШҜЩҲ ШЁШұ ШӯШіШЁЩҗ $z$ Ш§ШіШӘ. Щ…ЩӮШҜШ§ШұЩҗ $z$ ШЁШұ ШӯШіШЁЩҗ $x$ ШЁШұШ§ШЁШұ ШЁШ§
$$\frac{\frac{5}{12}x\pm\sqrt{(\frac{5}{12}x)^2+4x}}{2}$$
Щ…ЫҢвҖҢШҙЩҲШҜ Ъ©ЩҮ ШӘЩӮШұЫҢШЁЫҢ Ш§ШІ ШўЩҶ $\frac{\pm\sqrt{4x}}{2}$ ЫҢШ№ЩҶЫҢ $\pm\sqrt{x}$ Щ…ЫҢвҖҢШҙЩҲШҜ. Ш§ЫҢЩҶ ЫҢШ№ЩҶЫҢ ШЁЩҮ Ш§ШІШ§ЫҢ ЩҮШұ Щ…ЩӮШҜШ§ШұЩҗ ШҜЩ„Ш®ЩҲШ§ЩҮЫҢ Ш§ШІ $x$ (ШәЫҢШұ Ш§ШІ ШөЩҒШұ) Ш§ЩҶШӘШ®Ш§ШЁЫҢ ШЁШұШ§ЫҢ Щ…ЩӮШҜШ§ШұЩҗ $y$ Щ…ЫҢвҖҢШӘЩҲШ§ЩҶ ЫҢШ§ЩҒШӘ Ъ©ЩҮ Щ…ЩӮШҜШ§ШұЩҗ $z$ ШӘЩӮШұЫҢШЁШ§ ШЁШұШ§ШЁШұ ШЁШ§ $\sqrt{x}$ ЩҲ ЫҢШ§ $-\sqrt{x}$ ШҙЩҲШҜШҢ ЩҫШі ШЁШ§ Ш§ЩҒШІШ§ЫҢШҙ $x$ Щ…ЫҢвҖҢШӘЩҲШ§ЩҶ Ъ©Ш§ШұЫҢ Ъ©ШұШҜ Ъ©ЩҮ $z$ ЩҮШұ Ш№ШҜШҜ ШӯЩӮЫҢЩӮЫҢЩҗ ЩҶШ§ШөЩҒШұЫҢ ШұШ§ Ш§ШӘШ®Ш§Ш° Ъ©ЩҶШҜ. ШЁШұШ§ЫҢ ЩҶЩ…ЩҲЩҶЩҮ Ш®Щ… ЩӮШұЩ…ШІШұЩҶЪҜ ШЁШ§Щ„Ш§ ШұШ§ Ш§ЪҜШұ ШҜШұ ШЁШ§ШІЩҮЩ” $-100\leq x\leq 100$ ЩҲ $-1000\leq y\leq 1000$ ЩҶЪҜШ§ЩҮ Ъ©ЩҶЫҢШҜШҢ Щ…ЫҢвҖҢШЁЫҢЩҶЫҢШҜ Ъ©ЩҮ $z$ЩҮШ§ЫҢ Щ…Щ…Ъ©ЩҶ ШӘЩ…Ш§Щ… ШЁШ§ШІЩҮЩ” $[-10,10]$ ШұШ§ ЩҫЩҲШҙШҙ Щ…ЫҢвҖҢШҜЩҮЩҶШҜ.