کافیه که شکل های این دو تابع را بکشید:
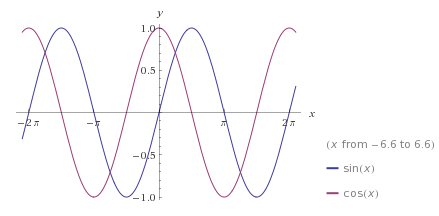
باید ببینیم کجا این دو تابع برابرند $\sin x=\cos x$ جواب این معادله برابر است با $x=k\pi +\frac\pi4, k\in\mathbb Z$ . با کمی توجه میبینید که در فواصل $2k\pi+\frac\pi4\leq x\leq (2k+1)\pi+\frac\pi4$ داریم $\cos x\leq \sin x$ و در بازه های $(2k-1)\pi+\frac\pi4\leq x\leq 2k\pi+\frac\pi4 $ داریم $\sin x\leq \cos x$ .
برای سوال دوم داریم
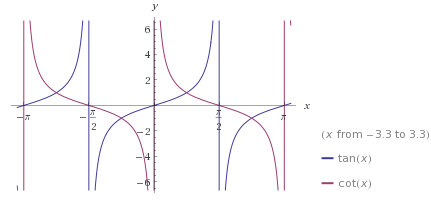
جاهایی که این دو همدیگر را قطع می کنند $\tan x=\cot x$ برابر است با $x=\frac{k\pi}2+\frac\pi4$ . با توجه با شکل در بازه های به شکل $k\pi< x\leq k\pi+\frac\pi4 $ و $k\pi+\frac\pi2< x\leq k\pi+\frac{3\pi}4$ داریم $\tan x\leq \cot x$ . و در بازه های $k\pi+\frac\pi4\leq x< k\pi+\frac\pi2$ و
$k\pi+\frac{3\pi}4\leq x< k\pi+\pi $ داریم $\tan x\geq \cot x$ .