به شکل زیر نگاه کنید:
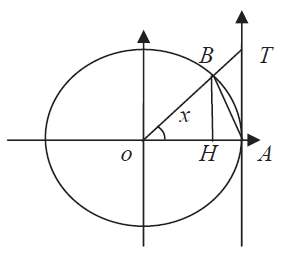
همانطور که می دانید $BH=\sin x$ و $AT=\tan x$. حال اگر مساحت های مثلث $OBH$ و قطاع $OBH$ و مثلث $OTA$ را مقایسه کنید داریم: $\frac 12\sin x\leq \frac12 x\leq \frac 12\tan x$ و لذا $\sin x\leq x\leq \tan x$ برای $0< x< \frac\pi2$. و همچنین برای $-\frac\pi2< x< 0$ نیز این نامساوی برقرار است.
می توان نشان داد برای هر $x$ نامساوی $|\sin x|\leq |x|$برقرار است. زیرا برای $x=0$ به وضوح تساوی برقرار است و برای $0< |x|< \frac\pi2$ بنابر آنچه در بالا آمد برقرار است و برای
$|x|>\frac\pi2>1\geq |\sin x|$.
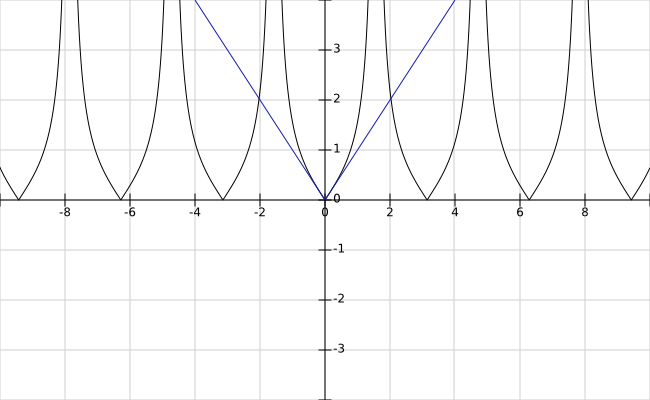
برای اینکه ببینیم $|x|\leq |\tan x|$ در کجا برقرار است می توانیم از نمودارهای $|\tan x|$ به رنگ سیاه و $|x|$ رنگ آبی استفاده کنیم: