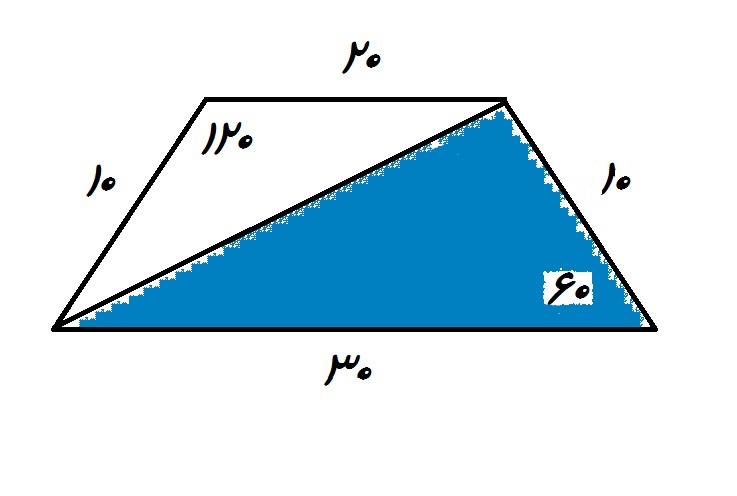
در هر مثلث اگر دو ضلع و زاویه بینشون معلوم باشد میتوان مساحت ان مثلث را به صورت زیر محاسبه کرد:
$$A= \frac{a.b.sin \beta }{2} $$
$$ A_{1} = \frac{10.30.sin60 }{2}= \frac{300 \sqrt{3} }{4} $$
$$ A_{2} = \frac{10.20.sin120 }{2}= \frac{200 \sqrt{3} }{4} $$
$$ A_{2} + A_{1}= \frac{500 \sqrt{3} }{4} $$
روش دوم:
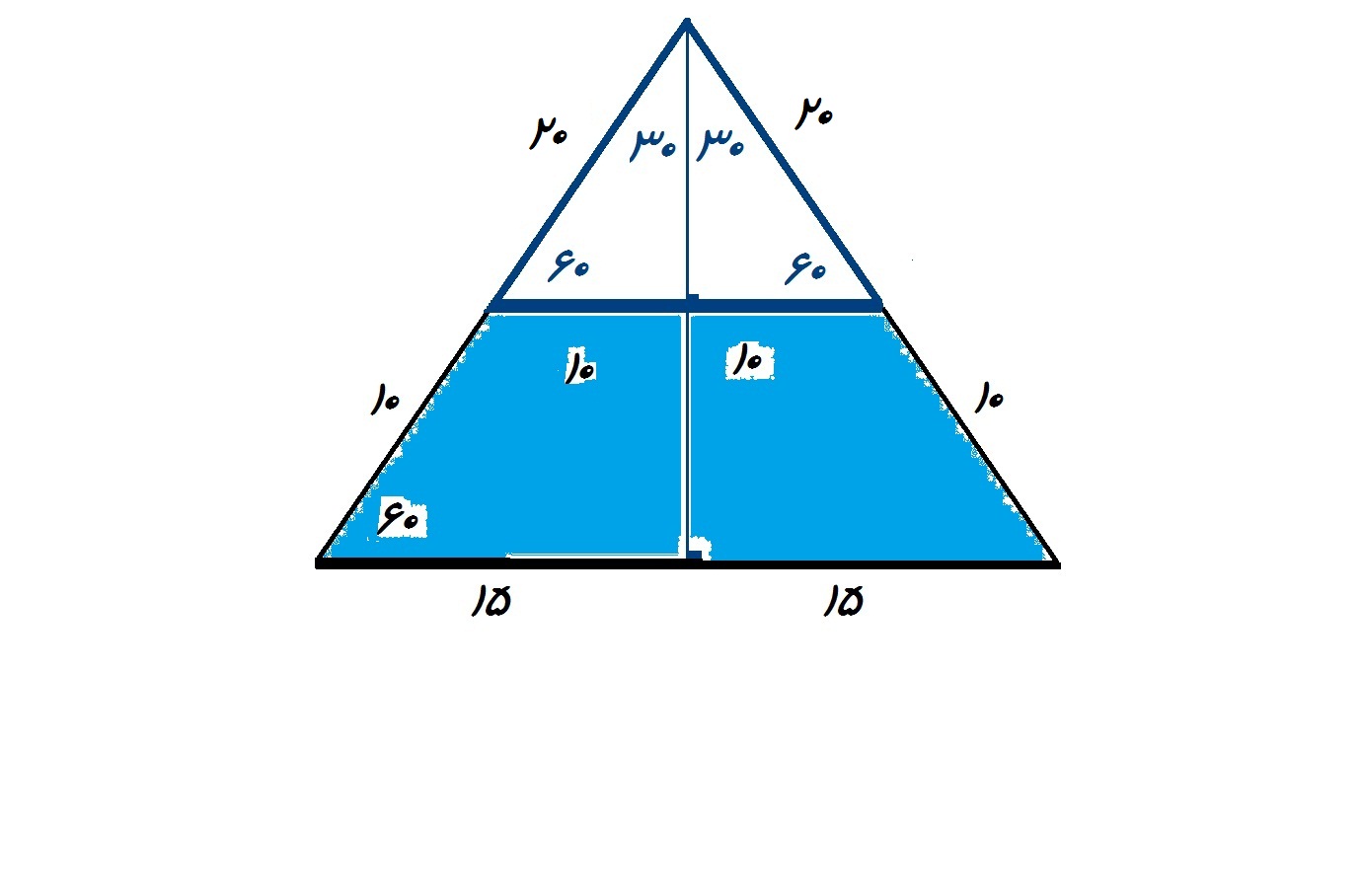
مساحت ذوزنقه=مساحت مثلث متساوی الضلاع بزرگ - مساحت مثلث متساوی الضلاع
$$A= \frac{(30)^2 \sqrt{3} }{4} - \frac{(20)^2 \sqrt{3} }{4}= \frac{500 \sqrt{3} }{4} $$
راه های دیگه هم وجود دارد که امید وارم دیگران انها را بررسی کنند!!