سلام
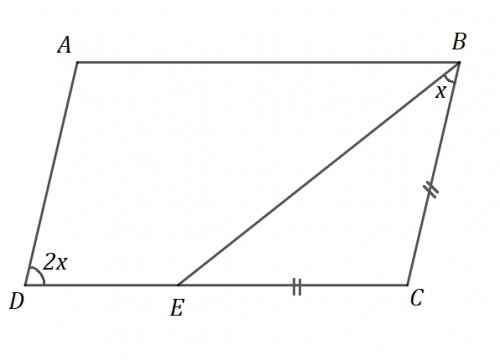
طبق تصور زاویه C محاسبه می شود:
$C+2x=180 \Rightarrow C=180-2x$
حال زاویه CEB را محاسبه می کنیم:
$CED=180-(C+x)=180-(180-2x+x)=x$
پس $BC=EC$. (چون $EBC=CEB$)
$S_{BCE}=\frac{1}{2}BC^2\sin(180-2x)=\frac{9}{2}\sin(2x)$
مساحت متوازی الاضلاع
$S_{ABCD}=2 \times \frac{1}{2}AD.DC\sin(2x)=3 \times 5\sin(2x)=15\sin(2x)$
در نتیجه:
$\frac{S_{BEC}}{S_{ABCD}}=\frac{\frac{9}{2}\sin(2x)}{15\sin(2x)}=\frac{3}{10}$
پس مساحت قسمت هاشور خورده $0.3$ برابر مساحت کل شکل است.