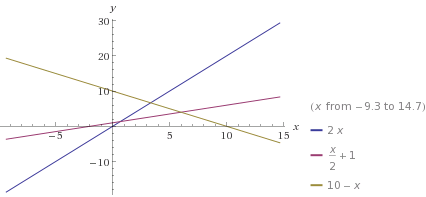
Щ…ЫҢ ШӘЩҲШ§ЩҶЫҢЩ… ШЁШұ Ш§ШіШ§Ші ШӯШ§Щ„Ш§ШӘ Ш§ШҙШӘШұШ§Ъ© ШіЩҮ Ш®Ш· ШҜШұ ШөЩҒШӯЩҮ Ъ©Щ„ЫҢЩҮ ШӯШ§Щ„Ш§ШӘ ШұШ§ ЩҫЫҢШҜШ§ Ъ©ЩҶЫҢЩ….
1- ШіЩҮ Ш®Ш· Щ…ЩҲШ§ШІЫҢ ШЁШ§ШҙЩҶШҜ: ЫҢШ№ЩҶЫҢ ШЁШ§ЫҢШҜ ШҙЫҢШЁ Ш®Ш· ЩҮШ§ ШЁШұШ§ШЁШұ ШЁШ§ШҙШҜ ЪҶЩҲЩҶ ШҙЫҢШЁ Ш®Ш· $ax+by=c$ ШЁШұШ§ШЁШұ Ш§ШіШӘ ШЁШ§ $\frac{-a}b$ Щ„Ш°Ш§ Щ…ЩҲШ§ШІЫҢ ШЁЩҲШҜЩҶ Ш®Ш·ЩҲШ· Щ…Ш№Ш§ШҜЩ„ Ш§ШіШӘ ШЁШ§ $\frac ab=\frac {a'}{b'}=\frac{a''}{b''}$
ШӘЩҲШ¬ЩҮ Ъ©ЩҶЫҢШҜ Ъ©ЩҮ ШҜШұ Ш§ЫҢЩҶ ШӯШ§Щ„ШӘ Ш§ШҙШӘШұШ§Ъ© Ш®Ш·ЩҲШ· ШӘЩҮЫҢ Ш§ШіШӘ.
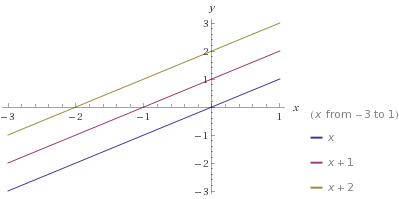
2- ШҜЩҲ Ш®Ш· Щ…ЩҶШ·ШЁЩӮ ЩҲ Ш®Ш· ШіЩҲЩ…ЫҢ ШЁШ§ ШўЩҶЩҮШ§ Щ…ЩҲШ§ШІЫҢ ШЁШ§ШҙШҜ: ШҜШұ Ш§ЫҢЩҶ ШӯШ§Щ„ШӘ Ш§ЩҲЩ„Ш§ Щ…Ш§ЩҶЩҶШҜ Ш§Щ„ЩҒ ШҙЫҢШЁ ЩҮШұ ШіЩҮ Ш®Ш· ШЁШұШ§ШЁШұ Ш§ШіШӘ Ш«Ш§ЩҶЫҢШ§ ШҜЩҲ Ш®Ш· Ш§ШІ Ш§ЫҢЩҶ ШіЩҮ Ш®Ш· ШҜШ§ШұШ§ЫҢ ЩҶЩӮШ·ЩҮ Ш§ШҙШӘШұШ§Ъ© ЩҮШіШӘЩҶШҜ.(ЫҢЪ© ЩҶЩӮШ·ЩҮ ШұЩҲЫҢ ЫҢЪ©ЫҢ Ш§ШІ Ш®Ш·ЩҮШ§ ШҜШұ ЩҶШёШұ Щ…ЫҢЪҜЫҢШұЫҢЩ… ЩҲ ШЁШұШұШіЫҢ Щ…ЫҢЪ©ЩҶЫҢЩ… Ъ©ЩҮ ШҜШұ Ъ©ШҜШ§Щ… ЫҢЪ© Ш§ШІ ШҜЩҲ Ш®Ш· ШҜЫҢЪҜШұ ШөШҜЩӮ Щ…ЫҢ Ъ©ЩҶШҜ)
ШҜШұ Ш§ЫҢЩҶ ШӯШ§Щ„ШӘ ЩҶЫҢШІ Ш§ШҙШӘШұШ§Ъ© Ш®Ш·ЩҲШ· ШӘЩҮЫҢ Ш§ШіШӘ.
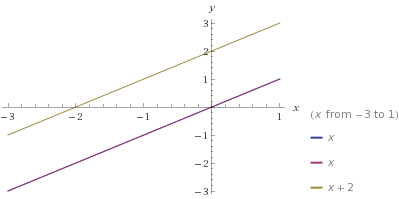
3- ШіЩҮ Ш®Ш· Щ…ЩҶШ·ШЁЩӮ ШЁШ§ШҙЩҶШҜ: ЫҢШ№ЩҶЫҢ ШҙЫҢШЁ ЩҮШұ ШіЩҮ ШЁШұШ§ШЁШұ Ш§ШіШӘ ЩҲ Ш«Ш§ЩҶЫҢШ§ ЩҮШұ ШіЩҮ Ш®Ш· ШҜШ§ШұШ§ЫҢ ЩҶЩӮШ·ЩҮ Ш§ШҙШӘШұШ§Ъ© ЩҮШіШӘЩҶШҜ.(ЫҢЪ© ЩҶЩӮШ·ЩҮ ШұЩҲЫҢ ЫҢЪ©ЫҢ Ш§ШІ Ш®Ш·ЩҲШ· ШҜШұ ЩҶШёШұ Щ…ЫҢЪҜЫҢШұЫҢЩ… ЩҲ ШЁШұШұШіЫҢ Щ…ЫҢЪ©ЩҶЫҢЩ… Ъ©ЩҮ ШҜШұ ШҜЩҲ Ш®Ш· ШҜЫҢЪҜШұ ЩҶЫҢШІ ШөШҜЩӮ Щ…ЫҢЪ©ЩҶШҜ)
Ш§ШҙШӘШұШ§Ъ© Ш®Ш·ЩҲШ· ШЁШұШ§ШЁШұ Ш§ШіШӘ ШЁШ§ Ш®ЩҲШҜ Ш§ЫҢЩҶ Ш®Ш·ЩҲШ·
4- ШіЩҮ Ш®Ш· ШҜШұ ЫҢЪ© ЩҶЩӮШ·ЩҮ Ш§ШҙШӘШұШ§Ъ© ШҜШ§ШҙШӘЩҮ ШЁШ§ШҙЩҶШҜ: ШӘЩҲШ¬ЩҮ Ъ©ЩҶЫҢШҜ ШҜШұ ШөЩҒШӯЩҮ ШҜЩҲ Ш®Ш· Ш§ЪҜШұ Щ…ЩҲШ§ШІЫҢ ЩҶШЁШ§ШҙЩҶШҜ ШҜШұ Ш§ЫҢЩҶШөЩҲШұШӘ Щ…ШӘЩӮШ§Ш·Ш№ Ш§ЩҶШҜ. ЩҫШі ШҙШұШ· ШӘЩӮШ§Ш·Ш№ ШҜШұ ЫҢЪ© ЩҶЩӮШ·ЩҮ Ш§ЫҢЩҶ Ш§ШіШӘ Ъ©ЩҮ ШҜЩҲ ШЁЩҮ ШҜЩҲ Ш§ЫҢЩҶ ШіЩҮ Ш®Ш· Щ…ШӘЩӮШ§Ш·Ш№ ШЁШ§ШҙЩҶШҜ ЩҲ Щ…Ш®ШӘШөШ§ШӘ ЩҶЩӮШ·ЩҮ ШӘЩӮШ§Ш·Ш№ ШҜШұ ШҜЩҲ ШЁЩҮ ШҜЩҲЫҢ ШўЩҶЩҮШ§ ЫҢЪ©ЫҢ ШЁШ§ШҙШҜ.
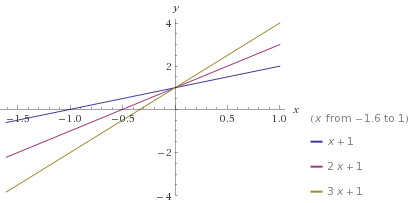
5- ШҜЩҲ Ш®Ш· Щ…ЩҲШ§ШІЫҢ ЩҲ Ш®Ш· ШіЩҲЩ… ШўЩҶЩҮШ§ ШұШ§ ЩӮШ·Ш№ Ъ©ЩҶШҜ: ШҜШұ Ш§ЫҢЩҶШөЩҲШұШӘ Ш§ШҙШӘШұШ§Ъ© Ш®Ш·ЩҲШ· ШЁШұШ§ШЁШұ ШҜЩҲ ЩҶЩӮШ·ЩҮ Ш§ШіШӘ. ШЁШұШ§ЫҢ ЩҫЫҢШҜШ§ Ъ©ШұШҜЩҶ ЩҶЩӮШ§Ш· ШӘЩӮШ§Ш·Ш№ ШЁШ§ЫҢШҜ ШҜЩҲ ШҜШіШӘЪҜШ§ЩҮ ШҜЩҲ Щ…Ш№Ш§ШҜЩ„ЩҮ ЩҲ ШҜЩҲ Щ…Ш¬ЩҮЩҲЩ„ЫҢ Ъ©ЩҮ ШЁШ§ Щ…Ш№Ш§ШҜЩ„ЩҮ Ш®Ш·ЩҲШ· Щ…ШӘЩӮШ§Ш·Ш№ ШӘШҙЪ©ЫҢЩ„ Щ…ЫҢ ШҙЩҲШҜ ШӯЩ„ Ъ©ЩҶЫҢШҜ.
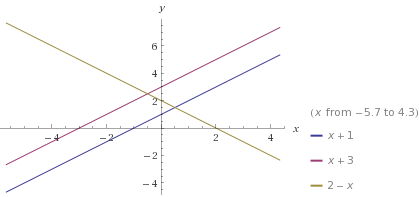
6- ШіЩҮ Ш®Ш· ШҜШұ ШіЩҮ ЩҶЩӮШ·ЩҮ Ш§ШҙШӘШұШ§Ъ© ШҜШ§ШҙШӘЩҮ ШЁШ§ШҙЩҶШҜ: ШҜШұ Ш§ЫҢЩҶШөЩҲШұШӘ Ш§ЫҢЩҶ Ш®Ш·ЩҲШ· ШҜЩҲ ШЁЩҮ ШҜЩҲ Щ…ШӘЩӮШ§Ш·Ш№ ШЁЩҲШҜЩҮ ЩҲ Щ…Ш®ШӘШөШ§ШӘ Щ…ШӯЩ„ ШӘЩӮШ§Ш·Ш№ ШЁШ№ШҜ Ш§ШІ ШӯЩ„ ШҜШіШӘЪҜШ§ЩҮ ШҜЩҲ Щ…Ш№Ш§ШҜЩ„ЩҮ ШҜЩҲ Щ…Ш¬ЩҮЩҲЩ„ЫҢ ШӘШҙЪ©ЫҢЩ„ ШҙШҜЩҮ ШӘЩҲШіШ· Ш§ЫҢЩҶ Ш®Ш·ЩҲШ· ШЁШ§ ЩҮЩ… ШҜЫҢЪҜШұ ШЁШұШ§ШЁШұ ЩҶЫҢШіШӘЩҶШҜ.