کافی است دقت کنید که دو منحنی با هم برابرند هرگاه متغیرهای $x$ و $y$ آنها با هم برابر باشند.
ثانیا دو خط بر هم عمودند هرگاه حاصلضرب شیب هاشان برابر منفی یک شود.
پس برای دو منحنی دلخواه از این دسته ها مثل $y=ax^3$ و $x^2+3y^2=b$ اولا در نقاط تماس $x$ و $y$ آنها برابرند ثانیا حاصلضرب شیب خط مماسشان را باید به دست آوریم(باید ثابت کنیم برابر منفی ک می شود)
شیب خط مماس در منحنی $y=ax^3$ در هر نقطه $x$ برابر است با مشتق آن در این نقطه $y'=3ax^2$ و از طرفی شیب خط مماس بر منحنی $x^2+3y^2=b$ در استفاده از مشتق ضمنی برابر است با $ y'= -\frac x {3y} $
در اینصورت حاصلضرب شیبها برابر است با $3ax^2\times (-\frac x {3y})=-\frac {ax^3}{y}$
اما در نقطه تماس $y$ در هر دو معادله منحنی صدق می کند از جمله $y=ax^3$ بنابر این حاصلضرب شیب ها برابر $-1$ می شود.
به عنوان مثال برای $a=1$ و $b=5$ من شکل رو رسم کردم:
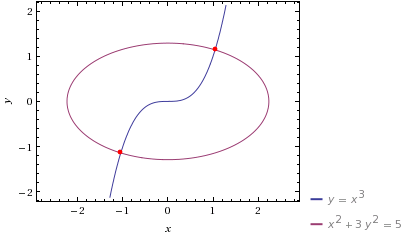
(عکس از wolframalpha)