فرض کنید $M(x_0, y_0)$ نقطه ای خارج از دایره به معادله $(x-a)^2+(y-b)^2=r^2$ باشد.
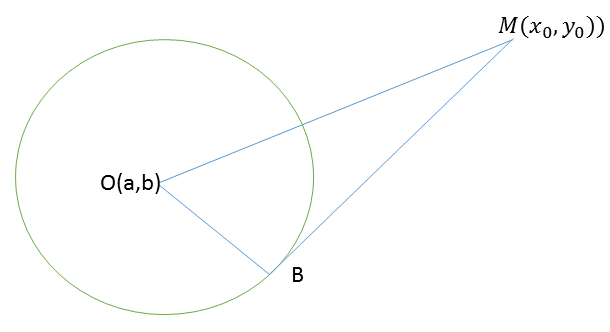
اگر از $M$ بر دایره مماس کنیم در اینصورت طبق شکل زیر یک مثلث قائم الزاویه تشکیل می شود. با استفاده از قضیه فیثاغوث داریم:
$$|MB|^2=|OM|^2-|OB|^2=(x_0-a)^2+(y_0-b)^2-r^2$$