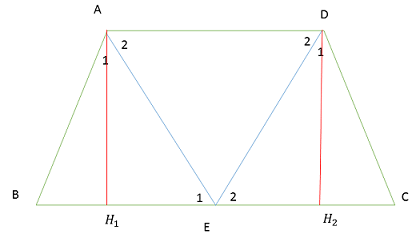
بنابرفرض مساله $\angle A_1=\angle A_2$ و $\angle B_1=\angle B_2$
اما در ذوزنقه، قاعده ها با هم موازی اند لذا طبق قضیه خطوط موازی $\angle A_2=\angle E_1$ و $\angle D_2=\angle E_2$
از تساوی های بالا نتیجه می شود $\angle A_1=\angle E_1$و $\angle D_1=\angle E_2$ بنابراین $AB=BE$و $CD=CE$ .
بنابرفرضیات مساله $AH_1=DH_2=12$ و $AE=15$و $DE=13$ .
بنابرقضیه فیثاغورث در مثلث $\triangle AH_1E$ داریم
$$H_1E=\sqrt{15^2-12^2}=\sqrt{81}=9$$
و لذا بنابرقضیه فیثاغورث در مثلث $ABH_1$ داریم
$$ AB^2=BE^2=(BH_1+H_1E)^2=AH_1^2+BH_1^2=144+BH_1^2 $$
با حل معادله $(BH_1+9)^2=144+BH_1^2$ داریم $18BH_1+81=144$ یا $BH_1=\frac{63}{18}=\frac{7}{2}$ .
بنابراین $AB=BH_1+H_1E=\frac{7}{2}+9$
و به طور مشابه می توانید اضلاع دیگر را بیابید.