بنابر شکل زیر دایره مثلثاتی(دایره به شعاع یک واحد) را در نظر بگیرید.
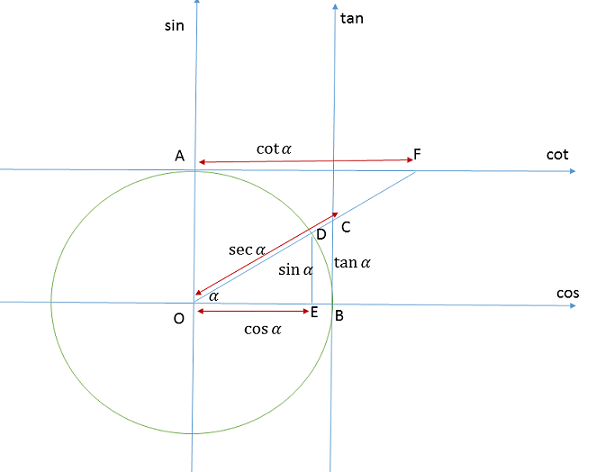
همانطور که در شکل مشخص شده داریم $DE=\sin \alpha$ و $OE=\cos \alpha$ و $BC=\tan\alpha$.
حال در مثلث $OBC$ چون $DE\|BC$ پس بنابر قضیه قالس و نتایج آن داریم
$$\frac{OE}{OB}=\frac{OD}{OC}$$
با جاگذاری موارد بالا داریم
$$\frac{\cos \alpha}{1}=\frac{1}{OC}$$
بنابراین $OC=\frac{1}{\cos\alpha}=\sec\alpha$ .
به همین ترتیب میتونید $\csc\alpha$ رو پیدا کنید؟