کمترین مساحت ممکن برای این چهارضلعی؟

Question

در چهارضلعی ABCD که نقطه O محل برخورد قطر هاست ، مساحت ABO برابر 8 و مساحت DCO برابر 18 است.کمترین مساحت ممکن برای این چهارضلعی چقدر است؟

1) 50

2)45

3)75

4) نمیتوان تعیین کرد.

Answer 1

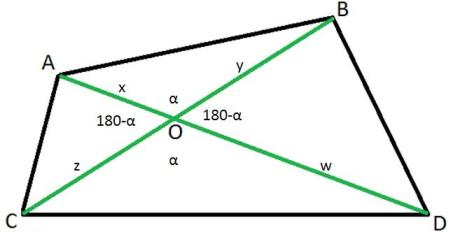
طبق فرض داریم: $$ S_{OAB} = \frac{1}{2} xy\ sin( \alpha )=8$$ وهمچنین: $$ S_{OCD} = \frac{1}{2} zw\ sin( \alpha )=18$$

پس برای مینیمم شدن مساحت باید $ S_{OBD} +S_{OCA}$ را مینیمم کنیم میدانیم $$ S_{OBD}= \frac{1}{2} yw\ sin( 180-\alpha )= \frac{1}{2} yw\ sin( \alpha ) $$ و $$S_{OCA} \frac{1}{2} xz\ sin( 180-\alpha )= \frac{1}{2} xz\ sin( \alpha ) $$ پس $$ S_{OCA} \times S_{OBD}= \frac{1}{2} yw\ sin( \alpha ) \times \frac{1}{2} xz\ sin( \alpha )= $$ $$ \frac{1}{2} xy\ sin( \alpha ) \times \frac{1}{2} zw\ sin( \alpha )=8 \times 18=144$$ حاصلضرب دو مساحت مقداری ثابت است پس مجموع زمانی مینیمم است که هر دو برابر باشند یعنی هر کدام برابر $12$ باشند.

مساحت کل مینیمم هم برابر است با: $$ 12+12+8+18=50$$

Comments

پاسخ این سوال را یکی از دبیران ریاضی فرستادند بنده فقط جواب رو تایپ کردم.

---

در هر صورت هم پاسخ و هم تایپ شما ارزشمند است

Answer 2

به نام خدا با سلام ،بنده یک اثبات دیگر نیز برایش دارم که عبارت است از: مقدار مساحت کل چهار ضلعی برابر است با: $S(ABO)+S(DCO)+S(BDO)+S(ACO) $که مقادیر $ S(ABO) $و$S(DCO)$داده شده است،پس $ S_{کل} $زمانی کم ترین مقدار است که :$ S(BDO)+S(ACO) $کمترین مقدار باشد.پس داریم:

$S(BDO)=S(ABO). \frac{DO}{AO} $و $S(AOC)=S(ODC). \frac{AO}{DO} $در کل حکم صورت سوال به این شکل میشود: $ min [ \frac{8DO}{AO} + \frac{18AO}{DO} ] $ حال باید مینیمم را بیابیم: $ \frac{8DO}{AO} + \frac{18AO}{DO}=t $برای سهولت کار $ DO=x،AO=y $خواهیم داشت: $ 8 x^{2}-txy+18 y^{2} =o $که در آخر برای یافتن ریشه به این روش عمل میکنیم: $ \frac{ty \pm \sqrt{ t^{2} y^{2}-4 \times 8 \times 18 y^{2} } }{16} $ که در اینجا حداقل $ t $برای اینکه این معادله ریشه موهومی نداشته باشد و در اعداد حقیقی جوابی داشته باشد بدست خواهد آمد :$ \sqrt{4 \times 8 \times 18}=24 $ دقت کنید که 24 حداقل مقدار مساحت دو مثلث مذکور است پس مساحت کل : $24+8+18=50 $

Comments

خیلی ممنون بابت پاسخ .
چه خوب میشه اگر در سایت ثبت نام کنید وقتتون زیاد گرفته نمیشه !!

Answer 3

جواب ۵۰ می شود زیرا از آنجایی که شکل مختلف الاضلاع است و قطر ها ان ها را نصف کرده اند و نه با این فرض که ABO با ACO وOBD با OCD مساوی باشند می توان گفت که ۲×۱۸ و ۲×۸ می شود و جمع که شوند ۵۲ می شود پس تقریبا جواب ۵۰ می شود. این روش ها روش های تست زنی کنکوری هستش که نیاز به تمرین زیاد داره...