به شکل زیر توجه کنید:
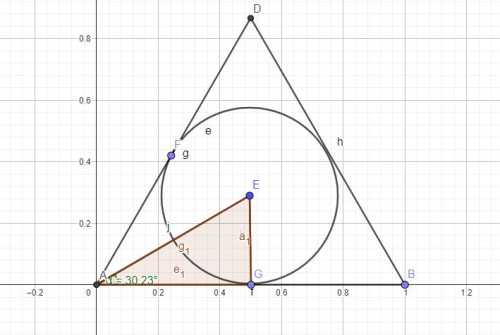
در مثلثی کوچک AEG که یک مثلث قائم الزاویه است (I) می دانیم که زاویه A نصف 60 درجه یعنی 30 درجه است. طول AG نیز با توجه به اینکه نصف طول ضلع مثلث است برابر با 0/5 خواهد بود. بنابراین ما یک زاویه و یک ضلع را در یک مثلث قایم الزاویه داریم. لذا می توانیم با نسبت های مثلثاتی مابقی مقادیر را پیدا کنیم.
$tan(A) = \frac{EG}{AG}= \frac{EG}{ \frac{1}{2} }
\Rightarrow
tan(30^{0} ) = \frac{ \sqrt{3} }{3}= \frac{EG}{ \frac{1}{2} }
$
اگر طرفین وسطین کنیم خواهیم داشت:
$ EG= \frac{\sqrt{3}}{6} $
همانطور که در شکل مشخص است EG همان شعاع دایره است. بنابراین مساحت دایره برابر خواهد بود با:
$S= \pi (\frac{\sqrt{3}}{6})^{2}= \pi \frac{3}{36} = \frac{\pi }{12} $
قضیه (I): شعاع دایره در نقطه تماس بر خط مماس عمود است. لذا پاره خط EG که شعاع دایره است بر خط مماس که ضلع AB است عمود است